In the part of the project that deals with Frobenius groups, we want to
- explicitly state the irreducible representations of fixed-point-free automorphism groups over finite fields.
- characterize classes of Frobenius groups with non-abelian kernel beyond the construction of individual examples as in [KW91,Aic01].
- compare the classical constructions with the construction via planar near-rings (Frobenius groups) in order to find out which approach is more efficient;
- determine which of the BIB-designs from planar near-rings are new.
In [Mod89] it is conjectured that the automorphism group of a
design ![]() defined as in 2.1.2 is of the form
defined as in 2.1.2 is of the form
![]() with
with ![]() the additive group of the near-ring,
the additive group of the near-ring, ![]() the
fixed-point-free automorphism group used to obtain the near-ring multiplication, and
the
fixed-point-free automorphism group used to obtain the near-ring multiplication, and
![]() the normalizer of
the normalizer of ![]() in the automorphism group
in the automorphism group ![]() of
of ![]() .
.
This conjecture in its full generality could already be refuted using SONATA. We now want to
- determine for which isomorphism types of the corresponding Frobenius group (in particular of the Frobenius complement) Modisett's conjecture is valid;
- determine whether the automorphism group of
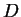 can always be expressed
as a semi-direct product of
can always be expressed
as a semi-direct product of 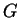 and a subgroup of
and a subgroup of 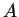 including the normalizer
of
including the normalizer
of 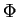 .
A positive answer to this question was given under certain additional
conditions on the design [KK94].
.
A positive answer to this question was given under certain additional
conditions on the design [KK94].
- characterize which Frobenius groups give isomorphic designs.
- find the connection between the structure theorems
on
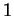 -primitive near-rings and those on planar near-rings;
-primitive near-rings and those on planar near-rings;
- generalize the description of
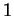 -primitive
near-rings to
-primitive
near-rings to 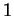 -primitive composition algebras, and
find generalizations of planar near-rings that
also yield geometric structures;
-primitive composition algebras, and
find generalizations of planar near-rings that
also yield geometric structures;
- characterize the
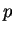 -groups
-groups 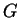 and fixed-point-free automorphism groups
and fixed-point-free automorphism groups 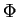 on
on
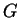 such that the sub-near-ring of
such that the sub-near-ring of 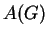 generated by the elements of
generated by the elements of
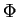 by pointwise addition and composition is local.
by pointwise addition and composition is local.
We want to
- determine the polynomial functions of Frobenius group by using the results in [Aic01];
- determine
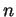 -ary polynomial functions on Frobenius groups;
-ary polynomial functions on Frobenius groups;
- find the compatible functions on Frobenius groups;
- characterize the affine complete Frobenius groups, that is Frobenius groups for which every compatible function is polynomial.