For the construction of Frobenius groups with non-abelian kernel, there is no systematic approach known. Examples of such groups have been described, e.g., in [KW91,Aic01].
Some near-rings (Frobenius groups) yield circular designs, that is,
designs where any two blocks intersect in at most two points.
In this case, the corresponding near-rings (Frobenius groups) are called
circular as well.
The combinatorial structure of circular designs has been investigated in
[Ke92,KK96].
As an example of the interplay between design and group structure, it is shown
in [BFK96] that only Frobenius groups with metacyclic
complement give circular designs.
Moreover, in that paper it is shown that
if
![]() is circular for a
is circular for a ![]() -group
-group ![]() , then all Frobenius
groups
, then all Frobenius
groups
![]() with
with ![]() a
a ![]() -group (same
-group (same ![]() , same
, same ![]() ) are circular.
The question remains open whether for any metacyclic group
) are circular.
The question remains open whether for any metacyclic group ![]() which
admits a fixed-point-free action, there exists a group
which
admits a fixed-point-free action, there exists a group ![]() such that
such that
![]() yields a circular design.
yields a circular design.
In [Pil96] applications of BIB-designs for statistical purposes (experimental design and analysis) are presented.
- All planar near-rings can be constructed via Ferrero's method [Fer70].
- Every zero-symmetric
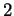 -primitive near-ring with unit is
either a ring, or it is dense in
a centralizer near-ring
-primitive near-ring with unit is
either a ring, or it is dense in
a centralizer near-ring
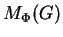 , where
, where
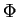 is a fixed-point-free automorphism group on
is a fixed-point-free automorphism group on 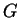 .
The
ideas used in the proof of this result
have been adapted to
.
The
ideas used in the proof of this result
have been adapted to 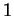 -primitive
near-rings without unit in [FP89].
-primitive
near-rings without unit in [FP89].
- Structural characterizations of planarity: For example,
a finite zero-symmetric near-ring
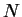 is integral and planar
iff it is subdirectly irreducible and
there is a natural number
is integral and planar
iff it is subdirectly irreducible and
there is a natural number 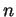 such that
such that
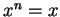 for all
for all 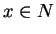 .
.
- Geometrical structures:
Planar near-rings give rise to geometrical structures,
namely BIB-designs.
It might be that similar structures can be obtained
from other classes of
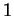 -primitive composition algebras.
-primitive composition algebras.