2.1.2 Introduction to near-rings

Planar near-rings form a special class of algebraic systems. Here is a short account on the basics of near-rings in general and planar near-rings in particular.

The set of all real functions, together with pointwise addition and composition, does not form a ring. Observe that ${(f+g)}\circ h = f\circ h + g\circ h$ holds by definition, while $f\circ(g+h)= f\circ g + f\circ h$ holds for all $g,h\in \mathbb{R}^{\mathbb{R}}$ if and only if $f$ is linear, i.e., if $f(x+y)=f(x)+f(y)$ for all $x,y\in \mathbb{R}$. Structures of the type like  $\mathbb{R}^{\mathbb{R}}$ are called near-rings:

Definition 1   A set $N$, together with two operations $+$ and $\circ$, is a near-ring provided that $(N,+)$ is a group (not necessarily abelian), $(N,\circ)$ is a semigroup, and $(n+n')\circ n'' = n\circ n''+n'\circ n''$ holds for all $n,n',n''\in N$.

Of course, every ring is a near-ring; hence near-rings are generalized rings. Two ring axioms are missing: the commutativity of addition and (much more important) the other distributive law.

Example 1   We have met the near-ring  $\mathbb{R}^{\mathbb{R}}$ already above. This and many other occasions show that near-rings form the ``nonlinear counterpart to ring theory''. More generally, take a group $(G,+)$; then $(G^{G},+,\circ)$ is a near-ring, and every near-ring can be embedded in some $(G^{G},+,\circ)$. More examples of near-rings are given by $(R[x],+,\circ)$, where $R$ is a commutative ring with identity, by the collection of continuous real functions, by the differentiable ones, or by the polynomial functions. Other important examples (see below) are centralizer near-rings $(\mathbf{M}_S(G),+,\circ) = \{f\colon G\to G\ \vert\ f\circ s=s\circ f$ for all $s\in S \}$, where $(G,+)$ is a group and $S\leq \textnormal{End}(G)$.

Actually, the first near-rings considered were near-fields, near-rings  $(N,+,\circ)$ in which $(N^{*},\circ)$ forms a group. In 1905, L. E. Dickson constructed the first proper near-fields by ``distorting'' the multiplication in a field. These types of near-fields are now called Dickson near-fields. Two years later, Veblen and Wedderburn used near-fields to coordinatize geometric planes. In a monumental paper, H. Zassenhaus showed in 1936 that all finite near-fields are Dickson ones, with the exception of 7 (well-known) cases. 51 years later, Zassenhaus showed that there do exist non-Dickson infinite near-fields of every prime characteristic.

For near-rings, we now have a sophisticated structure theory. Quite often, the results look similar to the ring case, but the proofs are completely different. For instance, matrix rings (``the stuff rings are made of'') have to be replaced by centralizer near-rings $(\mathbf{M}_S(G),+,\circ)$, where $S$ is a fixed-point free automorphism group.

These types of automorphisms turn up in another context as well; this one has nice applications to real-world problems.

Definition 2   A near-ring $N$ is called planar if all equations $x\circ a=x\circ b+c$ ( $a,b,c\in N$, not $x\circ a=x\circ b$ for all $x$), have exactly one solution $x\in N$.

This condition is motivated by geometry. It implies that two ``non-parallel lines $y=x\circ a + c_{1}$ and $y=x\circ b+c_{2}$ have exactly one point of intersection''. One example is $(\mathbb{C},+,*)$, where $a*b:=a\cdot\vert b\vert$. There are various methods to construct planar near-rings (see [Cla92,Pil83,Pil96]). Most of them use fixed-point-free automorphism groups; we just present the easiest way.

Definition 3   Construction method for finite planar near-rings. Take a finite field  $\mathbb{F}[q]$ and choose a generator $g$ for its multiplicative group. Choose a factorization $q-1=st$. Define a new multiplication $*_{t}$ in  $\mathbb{F}[q]$ as $g^{a}*_{t}g^{b} := g^{a+b-b_{t}}$, where $b_{t}$ denotes the remainder of $b$ on division by $t$; if one factor is 0, the product should be 0. Then $(\mathbb{F}[q],+,*_{t})$ is a planar near-ring.

Example 2   We choose $\mathbb{F}[7]$, and $t=2$ as divisor of $7-1$, so $g=3$ serves well as a generator. From this, we get the multiplication table

$$\begin{array}{c\vert ccccccc} *_{2} & 0 & 1 & 2 & 3 & 4 & 5 & 6 \... ... 5 & 0 & 5 & 3 & 5 & 6 & 6 & 3 \\ 6 & 0 & 6 & 5 & 6 & 3 & 3 & 5 \end{array}$$

Example 3   We want to test combinations of  $7$ ingredients for fertilizers. Testing all possible combinations of ingredients requires a huge amount of space and money. So we conduct an incomplete test; but this one should be fair to the ingredients (each ingredient should be applied the same number of times) and fair to the experimental fields (each test-field should get the same number of ingredients). We take the above near-ring of order  $7$ and form the sets $B_{i}=a*_{2}N^{*}+b$, $a\not\equiv 0$, and abbreviate $a*_{2}b$ by $ab$:

$$\begin{array}{rlrl} 1N^{*} + 0 & = \{1,2,4\}=:B_{1}, & 3N^{*} + ... ...{*} + 6 & = \{0,1,3\}=:B_{7}, & 3N^{*} + 6 & = \{2,4,5\}=:B_{14}. \end{array}$$

We see: these blocks form a so-called balanced incomplete block design (BIB-design) with $v=7$ points (namely $0,1,2,3,4,5,6$) and $b=14$ blocks; each point lies in exactly $r=6$ blocks; each block contains precisely $k=3$ elements, and every pair of different points appears in $\lambda=2$ blocks. ($v$,$b$,$r$,$k$,$\lambda$) are called the parameters of the design. In order to solve our fertilizer problem, we divide the whole experimental area into $14$ experimental fields, which we number by $1,2, \dots, 14$. We then apply precisely the fertilizers $F_{i}$ to a field $k$ if $i\in B_{k}$, $i=0,1,2, \dots 6$.

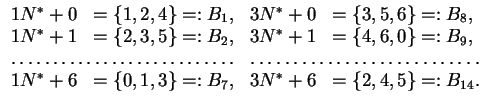
Field

1

2

3

4

5

6

7

8

9

10

11

12

13

14

Fertilizer

$F_{0}$

x

x

x

x

x

x

$F_{1}$

x

x

x

x

x

x

$F_{2}$

x

x

x

x

x

x

$F_{3}$

x

x

x

x

x

x

$F_{4}$

x

x

x

x

x

x

$F_{5}$

x

x

x

x

x

x

$F_{6}$

x

x

x

x

x

x

Yields:

2.8

6.1

1.2

8.5

8.0

3.9

7.7

5.5

4.0

10.7

3.2

4.9

3.8

5.5

The last row indicates the yields on the experimental fields after performing the experiment. Then we get: every field contains exactly $3$ fertilizers, and every fertilizer is applied to $6$ fields. Finally, every pair of different fertilizers is applied precisely twice in direct competition. Hence planar near-rings even have applications in agriculture!

The statistical analysis uses the incidence matrix  $\mathbf{A}$ of the design: compute $(\mathbf{A}\mathbf{A}^t)^{-1}\mathbf{A}\mathbf{y}^t=:(\beta_{0}, \dots ,\beta_{v-1})^t$. Then Linear Algebra tells us that $\beta_{0}, \dots, \beta_{v-1}$ are the best estimates for the effects of the ingredients $I_{0}, \dots, I_{v-1}$. In our case, we get the best estimates for the effects of $F_{0},\dots, F_{6}$ as $(3.6, 2.7, 0.3, 1.0, 0.1, 4.8, 0.1)$. If we take $F_{0},F_{1},F_{3},F_{5}$, we can expect a yield of $3.6+2.7+1.0+4.8=12.1$, which is considerably better than the yields $y_{i}$ which we got in our experiment. A more detailed statistical analysis gives confidence intervals for the effects of $F_{i}$, as well as information concerning their synergy effects.

Even more can be done with incidence matrices coming from BIB-Designs. The rows in the matrix  $\mathbf{A}$ are $0{-}1$-sequences, so they can be taken as a binary code  $C_{\mathbf{A}}$. This is a nonlinear, constant weight $r$ and constant distance   $d=2(r-\lambda)$ code of length  $b$ with $v$ codewords. These codes have the largest number of codewords among all codes with equal weight $r$, length $b$, and fixed minimal distance  $d$. So they also solve discrete sphere packing problems!