

Next: 2.1.2 Introduction to near-rings
Up: 2.1 State of the
Previous: 2.1 State of the
We give a rough sketch of the objects we are concerned with and of their
interdependencies. Planar near-rings have been used to obtain certain
BIB-designs [Fer70].
Finite planar near-rings can be constructed from an
additive group 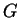 and a group
and a group 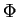 of automorphisms of
of automorphisms of 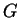 which act
fixed-point-freely on
which act
fixed-point-freely on 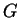 (see [AC68,Cla92,Pil83]).
This fact links planar near-rings and Frobenius groups. Each Frobenius group
is a semi-direct product of a group
(see [AC68,Cla92,Pil83]).
This fact links planar near-rings and Frobenius groups. Each Frobenius group
is a semi-direct product of a group 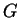 , the Frobenius kernel, which is
normal, and a fixed-point-free automorphism group
, the Frobenius kernel, which is
normal, and a fixed-point-free automorphism group 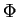 , the Frobenius complement
[Hup67].
, the Frobenius complement
[Hup67].
Fixed-point-free automorphism groups also occur in the characterization of
finite simple zero-symmetric near-rings with identity. Such a near-ring is
either a ring or isomorphic to a centralizer near-ring,
where 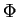 is a fixed-point-free automorphism group on the group
is a fixed-point-free automorphism group on the group 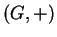 .
.
We plan to investigate the connections between near-rings, Frobenius groups
and designs. One goal is to reduce the properties of seemingly distinct
algebraic structures to one underlying concept, namely that of Frobenius
groups/fixed-point-free automorphism groups. This approach is meant to bridge the gaps
between classical topics which were investigated independently in the past.


Next: 2.1.2 Introduction to near-rings
Up: 2.1 State of the
Previous: 2.1 State of the
Peter Mayr
2002-08-12