The Presburger arithmetic, named after M. Presburger [Pre29] (translation: [Sta84]), is the first-order theory of natural numbers with a binary operation called addition. In 1929, M. Presburger proved the completeness and due to the constructive proof also the decidability with quantifier elimination. In this package the concepts of automata theory are used to decide Presburger arithmetic [Büc60].
‣ PredicataGrammar( ) | ( function ) |
The function PredicataGrammar returns the accepted grammar which is allowed as an input for PredicataFormula (3.1-4).
gap> PredicataGrammar(); The accepted grammar is defined as follows: <formula> ::= ( <formula> ) | ( <quantifier> <var> : <formula> ) | <formula> <logicconnective> <formula> | not <formula> | <term> = <term> | <var> <compare> <var> | <var> <compare> <int> | <int> <compare> <var> | <predicate> [ <varlist> ] | <predicate> | <boolean> <term> ::= ( <term> ) | <term> + <term> | <int> * <var> | ( - <int> ) * <var> | <var> | <int> <varlist> ::= <var> , <varlist> | <var> <quantifier>::= A | E <logicconnective>::= and | or | implies | equiv <compare> ::= < | <= | => | > | less | leq | geq | gr <var> ::= a | b | c | ... | x | y | z | a1 | ... | z1 | ... <int> ::= 0 | 1 | 2 | 3 | 4 | ... <boolean> ::= true | false <predicate> ::= P | Predicate1 | ... ; any name that isn't used above
‣ PredicataPredefinedPredicates( ) | ( function ) |
The function PredicataPredefinedPredicates() returns the predefined predicates which are allowed as an input for PredicataFormula (3.1-4).
gap> PredicataPredefinedPredicates(); Predefined predicates: * Buechi[x,y]: V_2(x)=y, where the function V_2(x) returns the highest power of 2 dividing x. * Power[x] : V_2(x)=x
‣ Predicaton( f ) | ( method ) |
The method Predicaton with a PredicataFormula f as an argument calls PredicataFormulaToPredicaton (3.4-1) and returns a minimal Predicaton.
gap> f:=PredicataFormula("2*x = y"); < PredicataFormula: 2 * x = y > gap> Predicaton(f); Predicaton: deterministic finite automaton on 4 letters with 3 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 ------------------------ [ 0, 0 ] | 1 3 3 [ 1, 0 ] | 2 3 3 [ 0, 1 ] | 3 1 3 [ 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. Regular expression of the automaton: ([ 1, 0 ][ 1, 1 ]*[ 0, 1 ]U[ 0, 0 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 3 states and the variable position list [ 1, 2 ]. >
‣ Predicaton( f, V ) | ( method ) |
The method Predicaton with a PredicataFormula f and a variable list V as arguments calls PredicataFormulaToPredicaton (3.4-1) and returns a minimal Predicaton.
gap> f:=PredicataFormula("2*x = y"); < PredicataFormula: 2 * x = y > gap> Predicaton(f, [ "y", "x" ]); Predicaton: deterministic finite automaton on 4 letters with 3 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 ------------------------ [ 0, 0 ] | 1 3 3 [ 1, 0 ] | 3 1 3 [ 0, 1 ] | 2 3 3 [ 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "y", "x" ]. Regular expression of the automaton: ([ 0, 1 ][ 1, 1 ]*[ 1, 0 ]U[ 0, 0 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 3 states and the variable position list [ 1, 2 ]. >
‣ Predicaton( S ) | ( method ) |
The method Predicaton with a String S as an argument calls StringToPredicaton (3.4-2) and returns a minimal Predicaton.
gap> Predicaton("(E y: x+y = z and x = y)"); Predicaton: deterministic finite automaton on 4 letters with 3 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 ------------------------ [ 0, 0 ] | 1 3 3 [ 1, 0 ] | 2 3 3 [ 0, 1 ] | 3 1 3 [ 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "z" ]. Regular expression of the automaton: ([ 1, 0 ][ 1, 1 ]*[ 0, 1 ]U[ 0, 0 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 3 states and the variable position list [ 1, 2 ]. >
‣ Predicaton( S, V ) | ( method ) |
The method Predicaton with a String S and a variable list V as arguments calls StringToPredicaton (3.4-2) and returns a minimal Predicaton.
gap> Predicaton("(E y: x+y = z and x = y)", [ "z", "x" ]); Predicaton: deterministic finite automaton on 4 letters with 3 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 ------------------------ [ 0, 0 ] | 1 3 3 [ 1, 0 ] | 3 1 3 [ 0, 1 ] | 2 3 3 [ 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "z", "x" ]. Regular expression of the automaton: ([ 0, 1 ][ 1, 1 ]*[ 1, 0 ]U[ 0, 0 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 3 states and the variable position list [ 1, 2 ]. >
‣ VariableListOfPredicaton( P ) | ( function ) |
The function VariableListOfPredicaton returns the variable list of a Predicaton P containing variable strings (see PredicataIsStringType (3.1-2)). Note that only the functions mentioned in this section preserve the variable list, since for the resizeable Predicata there are no reasons to implement it. There the variable position list may be increased but there's no information on how to increase the variable list, which usually will be eliminated again.
gap> P:=Predicaton("u3+2 = z5"); Predicaton: deterministic finite automaton on 4 letters with 4 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 --------------------------- [ 0, 0 ] | 3 2 2 4 [ 1, 0 ] | 2 2 3 2 [ 0, 1 ] | 2 2 4 2 [ 1, 1 ] | 3 2 2 4 Initial states: [ 1 ] Final states: [ 4 ] The alphabet corresponds to the following variable list: [ "u3", "z5" ]. Regular expression of the automaton: ([ 0, 0 ]U[ 1, 1 ])[ 1, 0 ]*[ 0, 1 ]([ 0, 0 ]U[ 1, 1 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 4 states and the variable position list [ 1, 2 ]. > gap> VariableListOfPredicaton(P); [ "u3", "z5" ]
‣ SetVariableListOfPredicaton( P ) | ( function ) |
The function SetVariableListOfPredicaton substitutes the variables of a Predicaton P with a new unique variables V. Here only the variable names are changed, compare with VariableAdjustedPredicaton (4.1-9) where the position of the variables, i.e. the variable position list is permuted.
gap> P:=Predicaton("x+y = z"); Predicaton: deterministic finite automaton on 8 letters with 3 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 --------------------------- [ 0, 0, 0 ] | 1 3 3 [ 1, 0, 0 ] | 3 2 3 [ 0, 1, 0 ] | 3 2 3 [ 1, 1, 0 ] | 2 3 3 [ 0, 0, 1 ] | 3 1 3 [ 1, 0, 1 ] | 1 3 3 [ 0, 1, 1 ] | 1 3 3 [ 1, 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y", "z" ]. Regular expression of the automaton: ([ 1, 1, 0 ]([ 1, 0, 0 ]U[ 0, 1, 0 ]U[ 1, 1, 1 ])* [ 0, 0, 1 ]U[ 0, 0, 0 ]U[ 1, 0, 1 ]U[ 0, 1, 1 ])* Output: < Predicaton: deterministic finite automaton on 8 letters with 3 states and the variable position list [ 1, 2, 3 ]. > gap> SetVariableListOfPredicaton(P, [ "z", "y", "x" ]); gap> Display(P); Predicaton: deterministic finite automaton on 8 letters with 3 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 --------------------------- [ 0, 0, 0 ] | 1 3 3 [ 1, 0, 0 ] | 3 2 3 [ 0, 1, 0 ] | 3 2 3 [ 1, 1, 0 ] | 2 3 3 [ 0, 0, 1 ] | 3 1 3 [ 1, 0, 1 ] | 1 3 3 [ 0, 1, 1 ] | 1 3 3 [ 1, 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "z", "y", "x" ].
‣ VariableAdjustedPredicaton( P, V ) | ( function ) |
The function VariableAdjustedPredicaton takes a Predicaton P and a permuted variable list V and returns the alphabet-permuted Predicaton corresponding to the old and the new variable list, each variable position of each variable may be changed. For \(x+y = z\) with [ "x", "y", "z" ] the function SetVariableListOfPredicaton (4.1-8) with [ "z", "y", "x" ] will change this to \(z+y = x\) but keep the automaton the same. Instead this function called with [ "z", "y", "x" ] won't change the formula \(x+y = z\) (with [ "x", "y", "z" ]) but instead changes the alphabet and the variable position list such that the variable "x" is set to the third position, "y" remains at the second position and "z" is set to the first position. Compare with PermutedAlphabetPredicaton (2.3-21) and SetVariablePositionListOfPredicaton (2.3-9).
gap> P:=Predicaton("x+y = z"); Predicaton: deterministic finite automaton on 8 letters with 3 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 --------------------------- [ 0, 0, 0 ] | 1 3 3 [ 1, 0, 0 ] | 3 2 3 [ 0, 1, 0 ] | 3 2 3 [ 1, 1, 0 ] | 2 3 3 [ 0, 0, 1 ] | 3 1 3 [ 1, 0, 1 ] | 1 3 3 [ 0, 1, 1 ] | 1 3 3 [ 1, 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y", "z" ]. Regular expression of the automaton: ([ 1, 1, 0 ]([ 1, 0, 0 ]U[ 0, 1, 0 ]U[ 1, 1, 1 ])* [ 0, 0, 1 ]U[ 0, 0, 0 ]U[ 1, 0, 1 ]U[ 0, 1, 1 ])* Output: < Predicaton: deterministic finite automaton on 8 letters with 3 states and the variable position list [ 1, 2, 3 ]. > gap> Q:=VariableAdjustedPredicaton(P, [ "z", "y", "x" ]);; gap> Display(Q); Predicaton: deterministic finite automaton on 8 letters with 3 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 --------------------------- [ 0, 0, 0 ] | 1 3 3 [ 1, 0, 0 ] | 3 1 3 [ 0, 1, 0 ] | 3 2 3 [ 1, 1, 0 ] | 1 3 3 [ 0, 0, 1 ] | 3 2 3 [ 1, 0, 1 ] | 1 3 3 [ 0, 1, 1 ] | 2 3 3 [ 1, 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "z", "y", "x" ].
‣ VariableAdjustedPredicata( P1, P2, V ) | ( function ) |
The function VariableAdjustedPredicata does the same as VariableAdjustedPredicaton (4.1-9) just for two Predicata P1 and P2 and a variable list V at the same time. Required for the next functions.
gap> P1:=Predicaton("x+y = z");; gap> P2:=Predicaton("y = 4");; gap> L:=VariableAdjustedPredicata(P1,P2, [ "x", "z", "y"]); [ < Predicaton: deterministic finite automaton on 8 letters with 3 states and the variable position list [ 1, 2, 3 ]. >, < Predicaton: deterministic finite automaton on 8 letters with 5 states and the variable position list [ 1, 2, 3 ]. > , [ 1, 2, 3 ] ] gap> VariableListOfPredicaton(L[1]); [ "x", "z", "y" ] gap> VariableListOfPredicaton(L[2]); [ "x", "z", "y" ]
‣ AndPredicata( P1, P2[, V] ) | ( function ) |
The function AndPredicata returns the intersection of the two Predicata P1 and P2 where the variable list (optional, by default V is the union of the variables of P1 and P2) defines the intersection and not the variable position. This function can be used to connect the Predicata of two formulas instead of calling Predicaton on the two with and connected formulas . In the example \(x+y = z\) and \(y = 4\), even if the variable "y" doesn't have the same variable position (in the first formula position 2 and in the second position 1), will be intersected regarding the variable names.
gap> P1:=Predicaton("x+y = z"); Predicaton: deterministic finite automaton on 8 letters with 3 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 --------------------------- [ 0, 0, 0 ] | 1 3 3 [ 1, 0, 0 ] | 3 2 3 [ 0, 1, 0 ] | 3 2 3 [ 1, 1, 0 ] | 2 3 3 [ 0, 0, 1 ] | 3 1 3 [ 1, 0, 1 ] | 1 3 3 [ 0, 1, 1 ] | 1 3 3 [ 1, 1, 1 ] | 3 2 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y", "z" ]. Regular expression of the automaton: ([ 1, 1, 0 ]([ 1, 0, 0 ]U[ 0, 1, 0 ]U[ 1, 1, 1 ])* [ 0, 0, 1 ]U[ 0, 0, 0 ]U[ 1, 0, 1 ]U[ 0, 1, 1 ])* Output: < Predicaton: deterministic finite automaton on 8 letters with 3 states and the variable position list [ 1, 2, 3 ]. > gap> P2:=Predicaton("y = 4"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 2 2 3 5 [ 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "y" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> P:=AndPredicata(P1, P2, [ "x", "y", "z"]);; gap> Display(P); Predicaton: deterministic finite automaton on 8 letters with 6 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 6 ------------------------------------ [ 0, 0, 0 ] | 1 2 2 2 4 5 [ 1, 0, 0 ] | 2 2 3 2 2 2 [ 0, 1, 0 ] | 2 2 2 2 2 2 [ 1, 1, 0 ] | 2 2 2 3 2 2 [ 0, 0, 1 ] | 2 2 1 2 2 2 [ 1, 0, 1 ] | 1 2 2 2 4 5 [ 0, 1, 1 ] | 2 2 2 1 2 2 [ 1, 1, 1 ] | 2 2 2 2 2 2 Initial states: [ 6 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y", "z" ]. gap> Q:=Predicaton("x+y = z and y = 4", [ "x", "y", "z"]); Predicaton: deterministic finite automaton on 8 letters with 6 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 6 ------------------------------------ [ 0, 0, 0 ] | 5 2 2 2 4 6 [ 1, 0, 0 ] | 2 2 3 2 2 2 [ 0, 1, 0 ] | 2 2 2 2 2 2 [ 1, 1, 0 ] | 2 2 2 3 2 2 [ 0, 0, 1 ] | 2 2 6 2 2 2 [ 1, 0, 1 ] | 5 2 2 2 4 6 [ 0, 1, 1 ] | 2 2 2 6 2 2 [ 1, 1, 1 ] | 2 2 2 2 2 2 Initial states: [ 1 ] Final states: [ 6 ] The alphabet corresponds to the following variable list: [ "x", "y", "z" ]. Regular expression of the automaton: ([ 0, 0, 0 ]U[ 1, 0, 1 ])([ 0, 0, 0 ]U[ 1, 0, 1 ]) ([ 1, 1, 0 ][ 1, 0, 0 ]*[ 0, 0, 1 ]U[ 0, 1, 1 ])([ 0, 0, 0 ]U[ 1, 0, 1 ])* Output: < Predicaton: deterministic finite automaton on 8 letters with 6 states and the variable position list [ 1, 2, 3 ]. >
‣ OrPredicata( P1, P2[, V] ) | ( function ) |
The function OrPredicata returns the union of the two Predicata P1 and P2 with the variable list (optional, by default V is the union of the variables of P1 and P2). This function can be used to connect the Predicata of two formulas instead of calling Predicaton on the two with or connected formulas.
gap> P1:=Predicaton("u = 4"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 2 2 3 5 [ 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "u" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> P2:=Predicaton("u = 2"); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 3 2 2 4 [ 1 ] | 2 2 4 2 Initial states: [ 1 ] Final states: [ 4 ] The alphabet corresponds to the following variable list: [ "u" ]. Regular expression of the automaton: [ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 4 states and the variable position list [ 1 ]. > gap> P:=OrPredicata(P1, P2);; gap> Display(P); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 1 2 2 5 3 [ 1 ] | 2 2 1 2 1 Initial states: [ 4 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "u" ].
‣ NotPredicaton( P[, V] ) | ( function ) |
The function NotPredicaton returns the negation of the Predicaton P. This function can be used to negate the Predicaton instead of calling Predicaton on the formula with prefix not. The optional parameter V allows to adjust the variable list (with VariableAdjustedPredicaton (4.1-9)).
gap> P:=Predicaton("x < 4"); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 3 2 4 4 [ 1 ] | 3 2 4 2 Initial states: [ 1 ] Final states: [ 1, 3, 4 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: ([ 0 ]U[ 1 ])(([ 0 ]U[ 1 ])[ 0 ]*U@)U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 4 states and the variable position list [ 1 ]. > gap> NotPredicaton(P);; gap> Display(P); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 3 2 4 4 [ 1 ] | 3 2 4 2 Initial states: [ 1 ] Final states: [ 2 ] The alphabet corresponds to the following variable list: [ "x" ].
‣ ImpliesPredicata( P1, P2[, V] ) | ( function ) |
The function ImpliesPredicata returns the implication of the Predicata P1 and P2 with variable list (optional, by default V is the union of the variables of P1 and P2). This function can be used to connect the Predicata of two formulas instead of calling Predicaton on the two with implies connected formulas.
gap> P1:=Predicaton("(E m: x = 4*m)"); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 4 2 3 3 [ 1 ] | 2 2 3 2 Initial states: [ 1 ] Final states: [ 1, 3, 4 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ]([ 0 ]([ 0 ]U[ 1 ])*U@)U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 4 states and the variable position list [ 1 ]. > gap> P2:=Predicaton("(E n: x = 2*n)"); Predicaton: deterministic finite automaton on 2 letters with 3 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 --------------------- [ 0 ] | 3 2 3 [ 1 ] | 2 2 3 Initial states: [ 1 ] Final states: [ 1, 3 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ]([ 0 ]U[ 1 ])*U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 3 states and the variable position list [ 1 ]. > gap> P:=ImpliesPredicata(P1, P2, [ "x" ]);; gap> Display(P); Predicaton: deterministic finite automaton on 2 letters with 1 state, the variable position list [ 1 ] and the following transitions: | 1 --------------- [ 0 ] | 1 [ 1 ] | 1 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x" ].
‣ EquivalentPredicata( P1, P2[, V] ) | ( function ) |
‣ EquivPredicata( P1, P2[, V] ) | ( function ) |
The function EquivalentPredicata returns the equivalence of the Predicata P1 and P2 with the variable list (optional, by default V is the union of the variables of P1 and P2). This function can be used to connect the Predicata of two formulas instead of calling Predicaton on the two with equiv connected formulas.
gap> P1:=Predicaton("(E y: 2*x = 7+3*y)"); Predicaton: deterministic finite automaton on 2 letters with 6 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 ------------------------------ [ 0 ] | 5 2 4 3 4 6 [ 1 ] | 4 3 6 4 2 3 Initial states: [ 1 ] Final states: [ 6 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: (([ 0 ][ 0 ]U[ 1 ])[ 1 ]*[ 0 ]U[ 0 ][ 1 ][ 0 ]*[ 1 ]) ([ 1 ][ 0 ]*[ 1 ]U[ 0 ][ 1 ]*[ 0 ])*[ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 6 states and the variable position list [ 1 ]. > gap> P2:=Predicaton("(E k: x = 5+3*k)"); Predicaton: deterministic finite automaton on 2 letters with 6 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 ------------------------------ [ 0 ] | 5 2 4 3 4 6 [ 1 ] | 4 3 6 4 2 3 Initial states: [ 1 ] Final states: [ 6 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: (([ 0 ][ 0 ]U[ 1 ])[ 1 ]*[ 0 ]U[ 0 ][ 1 ][ 0 ]*[ 1 ]) ([ 1 ][ 0 ]*[ 1 ]U[ 0 ][ 1 ]*[ 0 ])*[ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 6 states and the variable position list [ 1 ]. > gap> P:=EquivalentPredicata(P1, P2);; gap> Display(P); Predicaton: deterministic finite automaton on 2 letters with 1 state, the variable position list [ 1 ] and the following transitions: | 1 --------------- [ 0 ] | 1 [ 1 ] | 1 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x" ].
‣ ExistsPredicaton( P, v[, V] ) | ( function ) |
The function ExistsPredicaton returns the existence quantifier with the variable v applied on the Predicaton P. This function can be used to quantify the Predicaton instead of calling (E v: ...) on the formula. The optional parameter V allows to adjust the variable list (with VariableAdjustedPredicaton (4.1-9)).
gap> P:=Predicaton("5*x+6*y = n"); Predicaton: deterministic finite automaton on 8 letters with 12 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 ------------------------------------------------------ [ 0, 0, 0 ] | 1 2 2 3 4 5 2 7 2 2 12 2 [ 1, 0, 0 ] | 2 2 1 2 2 2 3 2 7 5 2 4 [ 0, 1, 0 ] | 2 2 7 2 2 2 5 2 8 9 2 12 [ 1, 1, 0 ] | 4 2 2 7 5 8 2 12 2 2 9 2 [ 0, 0, 1 ] | 7 2 2 5 12 9 2 8 2 2 6 2 [ 1, 0, 1 ] | 2 2 7 2 2 2 5 2 8 9 2 12 [ 0, 1, 1 ] | 2 2 8 2 2 2 9 2 10 11 2 6 [ 1, 1, 1 ] | 12 2 2 8 9 10 2 6 2 2 11 2 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "n", "x", "y" ]. Output: < Predicaton: deterministic finite automaton on 8 letters with 12 states and the variable position list [ 1, 2, 3 ]. > gap> P:=ExistsPredicaton(P, "x");; gap> P:=ExistsPredicaton(P, "y");; gap> Display(P); Predicaton: deterministic finite automaton on 2 letters with 12 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 ------------------------------------------------ [ 0 ] | 9 2 3 2 4 5 3 7 8 2 4 11 [ 1 ] | 12 3 3 2 3 2 2 2 10 7 7 6 Initial states: [ 1 ] Final states: [ 1, 3, 7, 8, 9 ] The alphabet corresponds to the following variable list: [ "n" ].
‣ ForallPredicaton( P, v[, V] ) | ( function ) |
The function ForallPredicaton returns the for all quantifier with the variable v applied on the Predicaton P. This function can be used to quantify the Predicaton instead of calling (A v: ...) on the formula. The optional parameter V allows to adjust the variable list (with VariableAdjustedPredicaton (4.1-9)).
gap> P1:=Predicaton("(E x: (E y: 5*x+6*y = n))"); Predicaton: deterministic finite automaton on 2 letters with 12 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 ------------------------------------------------ [ 0 ] | 12 2 4 5 2 2 5 7 9 9 10 11 [ 1 ] | 8 9 2 9 2 10 10 3 9 2 2 6 Initial states: [ 1 ] Final states: [ 1, 9, 10, 11, 12 ] The alphabet corresponds to the following variable list: [ "n" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 12 states and the variable position list [ 1 ]. > gap> P2:=Predicaton("n > 19"); Predicaton: deterministic finite automaton on 2 letters with 7 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 --------------------------------- [ 0 ] | 6 2 2 3 4 5 7 [ 1 ] | 6 7 2 2 3 5 7 Initial states: [ 1 ] Final states: [ 7 ] The alphabet corresponds to the following variable list: [ "n" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 7 states and the variable position list [ 1 ]. > gap> P3:=ImpliesPredicata(P2, P1);; gap> P:=ForallPredicaton(P3, "n");; gap> Display(P); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ]
‣ LeastAcceptedNumber( P[, b] ) | ( function ) |
The function LeastAcceptedNumber returns the Predicaton recognizing the least number which is accepted by the given Predicaton P. If the argument b is true (by default), then the Predicaton recognizing the least number greater \(0\) is returned (if there is one), otherwise \(0\) is included.
gap> P:=Predicaton("x >= 4"); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 3 2 2 4 [ 1 ] | 3 4 2 4 Initial states: [ 1 ] Final states: [ 4 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: ([ 0 ]U[ 1 ])([ 0 ]U[ 1 ])[ 0 ]*[ 1 ]([ 0 ]U[ 1 ])* Output: < Predicaton: deterministic finite automaton on 2 letters with 4 states and the variable position list [ 1 ]. > gap> L:=LeastAcceptedNumber(P); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 2 2 3 5 [ 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. >
‣ GreatestAcceptedNumber( P ) | ( function ) |
The function GreatestAcceptedNumber returns the Predicaton recognizing the greatest number which is accepted by the given Predicaton P.
gap> P:=Predicaton("(E x: 2*x = y and x < 9)"); Predicaton: deterministic finite automaton on 2 letters with 8 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 ------------------------------------ [ 0 ] | 3 2 7 4 4 5 6 5 [ 1 ] | 2 2 8 2 4 4 5 5 Initial states: [ 1 ] Final states: [ 1, 3, 4, 5, 6, 7, 8 ] The alphabet corresponds to the following variable list: [ "y" ]. Regular expression of the automaton: [ 0 ](([ 1 ]([ 0 ]U[ 1 ])U[ 0 ]([ 0 ][ 0 ]U[ 1 ])) (([ 0 ]U[ 1 ])[ 0 ]*U@)U[ 1 ]U[ 0 ]([ 0 ]([ 1 ][ 0 ]*U@)U@)U@)U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 8 states and the variable position list [ 1 ]. > gap> G:=GreatestAcceptedNumber(P); Predicaton: deterministic finite automaton on 2 letters with 7 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 --------------------------------- [ 0 ] | 6 2 2 3 4 5 7 [ 1 ] | 2 2 7 2 2 2 2 Initial states: [ 1 ] Final states: [ 7 ] The alphabet corresponds to the following variable list: [ "y" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 7 states and the variable position list [ 1 ]. >
‣ LeastNonAcceptedNumber( P ) | ( function ) |
The function LeastNonAcceptedNumber returns the Predicaton recognizing the Least number which is not recognized by the given Predicaton P.
gap> P:=Predicaton("x < 4 or x > 8"); Predicaton: deterministic finite automaton on 2 letters with 7 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 --------------------------------- [ 0 ] | 7 2 3 3 4 4 6 [ 1 ] | 5 3 3 2 4 2 4 Initial states: [ 1 ] Final states: [ 1, 3, 4, 5, 6, 7 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: ([ 0 ]([ 0 ][ 0 ]U[ 1 ])U[ 1 ]([ 0 ]U[ 1 ]))(([ 1 ][ 0 ]*[ 1 ]U[ 0 ]) ([ 0 ]U[ 1 ])*U@)U[ 0 ]([ 0 ]([ 1 ][ 0 ]*[ 1 ]([ 0 ]U[ 1 ])*U@)U@)U[ 1 ]U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 7 states and the variable position list [ 1 ]. > gap> L:=LeastNonAcceptedNumber(P); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 2 2 3 5 [ 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. >
‣ GreatestNonAcceptedNumber( P ) | ( function ) |
The function GreatestNonAcceptedNumber returns the Predicaton recognizing the greatest number which is not recognized by the given Predicaton P.
gap> P:=Predicaton("(E x: (E y: 3*x + 4*y = n))"); Predicaton: deterministic finite automaton on 2 letters with 6 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 ------------------------------ [ 0 ] | 6 2 2 3 5 5 [ 1 ] | 4 5 2 5 5 2 Initial states: [ 1 ] Final states: [ 1, 5, 6 ] The alphabet corresponds to the following variable list: [ "n" ]. Regular expression of the automaton: ([ 0 ]([ 1 ][ 0 ]*[ 1 ]U[ 0 ])U[ 1 ][ 0 ]([ 0 ]U[ 1 ]) [ 0 ]*[ 1 ]U[ 1 ][ 1 ])([ 0 ]U[ 1 ])*U[ 0 ]U@ Output: < Predicaton: deterministic finite automaton on 2 letters with 6 states and the variable position list [ 1 ]. > gap> G:=GreatestNonAcceptedNumber(P); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 2 2 2 3 5 [ 1 ] | 4 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "n" ]. Regular expression of the automaton: [ 1 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(G); [ [ 5 ] ]
‣ InterpretedPredicaton( P ) | ( function ) |
The function InterpretedPredicaton returns true if the Predicaton P has exactly one state which is also a final state, thus the Predicaton is interpreted as true (if free variable occurs it is true for all natural numbers). Otherwise, false is returned.
gap> P:=Predicaton("(A x: (E y: x = y))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ] Regular expression of the automaton: [ ]* Due to the automaton the formula is true. true Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> InterpretedPredicaton(P); The Predicaton is interpreted as True. true
‣ AreEquivalentPredicata( P1, P2[, b] ) | ( function ) |
The function AreEquivalentPredicata returns either true if the Predicatas P1 and P2 are equivalent or false otherwise. If the optional parameter b is true (by default) then the equivalence is computed w.r.t. the variable names, if false it is computed w.r.t. to the variable position list.
gap> P1:=Predicaton("x=4", ["x", "y"]); Predicaton: deterministic finite automaton on 4 letters with 5 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 5 ------------------------------ [ 0, 0 ] | 4 2 2 3 5 [ 1, 0 ] | 2 2 5 2 2 [ 0, 1 ] | 4 2 2 3 5 [ 1, 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. Output: < Predicaton: deterministic finite automaton on 4 letters with 5 states and the variable position list [ 1, 2 ]. > gap> P2:=Predicaton("u=4", ["u", "v", "w"]); Predicaton: deterministic finite automaton on 8 letters with 5 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 --------------------------------- [ 0, 0, 0 ] | 4 2 2 3 5 [ 1, 0, 0 ] | 2 2 5 2 2 [ 0, 1, 0 ] | 4 2 2 3 5 [ 1, 1, 0 ] | 2 2 5 2 2 [ 0, 0, 1 ] | 4 2 2 3 5 [ 1, 0, 1 ] | 2 2 5 2 2 [ 0, 1, 1 ] | 4 2 2 3 5 [ 1, 1, 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "u", "v", "w" ]. Output: < Predicaton: deterministic finite automaton on 8 letters with 5 states and the variable position list [ 1, 2, 3 ]. > gap> AreEquivalentPredicata(P1, P2); The Predicaton doesn't hold for all natural numbers and is interpreted as False. false gap> AreEquivalentPredicata(P1, P2, false); The Predicaton holds for all natural numbers and is interpreted as True. true
‣ LinearSolveOverN( A, b[, V] ) | ( function ) |
The function LinearSolveOverN returns the Predicaton which language recognizes the solutions \(x\) of the linear equation \(A \cdot x = b\). The argument A is a matrix (list of lists), the argument b a vector (list) and the optional argument V allows to specify an order (here the variables are named "x1", "x2", ...). Note that A and b may contain also negative integers, whereas the solution is over the natural numbers.
gap> A:=LinearSolveOverN([ [ 1, -2, 3 ], [ 3, 4, -7 ] ], [ 2, 0 ]); Predicaton: deterministic finite automaton on 8 letters with 17 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 --------------------------------------------------------------------- [ 0, 0, 0 ] | 2 2 2 2 4 2 2 2 8 2 10 2 2 2 2 2 17 [ 1, 0, 0 ] | 2 2 2 14 2 9 2 2 2 8 2 2 12 2 2 2 2 [ 0, 1, 0 ] | 11 2 17 2 2 2 2 7 2 2 2 8 2 2 2 2 2 [ 1, 1, 0 ] | 2 2 2 2 2 2 6 2 2 2 2 2 2 9 14 8 2 [ 0, 0, 1 ] | 2 2 2 3 2 4 2 2 2 16 2 2 15 2 2 2 2 [ 1, 0, 1 ] | 2 2 2 2 13 2 2 2 12 2 4 2 2 2 2 2 5 [ 0, 1, 1 ] | 2 2 2 2 2 2 17 2 2 2 2 2 2 4 3 16 2 [ 1, 1, 1 ] | 17 2 5 2 2 2 2 14 2 2 2 12 2 2 2 2 2 Initial states: [ 1 ] Final states: [ 17 ] The alphabet corresponds to the following variable list: [ "x1", "x2", "x3" ]. Output: < Predicaton: deterministic finite automaton on 8 letters with 17 states and the variable position list [ 1, 2, 3 ]. > gap> AcceptedByPredicaton(A, 10); [ [ 1, 1, 1 ], [ 2, 9, 6 ] ]
‣ NullSpaceOverN( A[, V] ) | ( function ) |
The function NullSpaceOverN returns the Predicaton which language recognizes the solutions \(x\) of the linear equation \(A \cdot x = 0\). The argument A is a matrix (list of lists) and the optional argument V allows to specify an order (here the variables are named "x1", "x2", ...). Note that A may contain also negative integers, whereas the solution is over the natural numbers.
gap> N:=NullSpaceOverN([[1, -2, 3],[3, 4, -7]]); Predicaton: deterministic finite automaton on 8 letters with 13 states, the variable position list [ 1, 2, 3 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 13 --------------------------------------------------------- [ 0, 0, 0 ] | 1 2 2 2 4 2 2 2 8 2 2 2 2 [ 1, 0, 0 ] | 2 2 2 12 2 9 2 2 2 2 10 2 2 [ 0, 1, 0 ] | 2 2 1 2 2 2 2 7 2 8 2 2 2 [ 1, 1, 0 ] | 2 2 2 2 2 2 6 2 2 2 2 9 12 [ 0, 0, 1 ] | 2 2 2 3 2 4 2 2 2 2 13 2 2 [ 1, 0, 1 ] | 5 2 2 2 11 2 2 2 10 2 2 2 2 [ 0, 1, 1 ] | 2 2 2 2 2 2 1 2 2 2 2 4 3 [ 1, 1, 1 ] | 2 2 5 2 2 2 2 12 2 10 2 2 2 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x1", "x2", "x3" ]. Output: < Predicaton: deterministic finite automaton on 8 letters with 13 states and the variable position list [ 1, 2, 3 ]. > gap> AcceptedByPredicaton(N); [ [ 0, 0, 0 ], [ 1, 8, 5 ] ]
The following example introduces the two ways of getting a Predicaton, either created from a first-order formula (see PredicataGrammar (4.1-1)), the mathematically more intuitive way, or from an Automaton, which at first sight may not completely obvious.
gap> # We want a Predicaton accepting the binary representation of the number 4: gap> DecToBin(4); [ 0, 0, 1 ] gap> A:=Predicaton("x = 4"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 2 2 3 5 [ 1 ] | 2 2 5 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> # Accepted natural numbers? gap> IsAcceptedByPredicaton(A, [ 4 ]); true gap> # Accepted binary representation, also with leading zero? gap> IsAcceptedByPredicaton(A, [ [ 0, 0, 1 ] ]); true gap> IsAcceptedByPredicaton(A, [ [ 0, 0, 1, 0 ] ]); true gap> # Indeed any leading zeros can be added or cancelled: gap> PredicatonToRatExp(A); [ 0 ][ 0 ][ 1 ][ 0 ]* gap> # Now we create the Predicaton recognizing "y = 1" by hand: gap> # Parameters: type, states, alphabet, gap> Aut:=Automaton("det", 3, [ [ 0 ], [ 1 ] ], > # transitions from letter (row) and state (column) to state (row, column) > [ [ 3, 2, 3 ], [ 2, 3, 3 ] ], > # initial state, final states > [ 1 ], [ 2 ]); < deterministic automaton on 2 letters with 3 states > gap> # We create the Predicaton from the automaton and the variable position list. gap> # Here we choose "y" to be at position 2. gap> B:=Predicaton(Aut, [ 2 ]); < Predicaton: deterministic finite automaton on 2 letters with 3 states and the variable position list [ 2 ]. > gap> # We want the Predicaton "x = 4 and y = 1", so we have to set a variable to B. gap> SetVariableListOfPredicaton(B, [ "y" ]); gap> # Then we use AndPredicata to apply "and" according to the variable names. gap> # Hence the Predicaton is over the alphabet [[0, 0], [1, 0], [0, 1], [1, 1]], gap> # where the first coordinate belong to "x" and the second to "y". Note that gap> # [ "x", "y" ] is optional, by default it's sorted alphabetically. gap> C:=AndPredicata(A, B, [ "x", "y" ]);; gap> Display(C); Predicaton: deterministic finite automaton on 4 letters with 5 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 5 ------------------------------ [ 0, 0 ] | 2 2 2 3 5 [ 1, 0 ] | 2 2 5 2 2 [ 0, 1 ] | 4 2 2 2 2 [ 1, 1 ] | 2 2 2 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. gap> # So C accepts in the first component of the letter the variable x gap> # and in the second component the variable y. gap> IsAcceptedByPredicaton(C, [ 4, 1 ]); true gap> IsAcceptedByPredicaton(C, [ [ 0, 0, 1 ], [ 1 ] ]); true gap> # Alternatively, we could have created this Predicaton simply with gap> D:=Predicaton("x = 4 and y = 1"); Predicaton: deterministic finite automaton on 4 letters with 5 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 5 ------------------------------ [ 0, 0 ] | 2 2 2 3 5 [ 1, 0 ] | 2 2 5 2 2 [ 0, 1 ] | 4 2 2 2 2 [ 1, 1 ] | 2 2 2 2 2 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. Regular expression of the automaton: [ 0, 1 ][ 0, 0 ][ 1, 0 ][ 0, 0 ]* Output: < Predicaton: deterministic finite automaton on 4 letters with 5 states and the variable position list [ 1, 2 ]. > gap> DrawPredicaton(D); gap> # Furthermore, we can use the following function to see the allowed grammar: gap> PredicataGrammar();

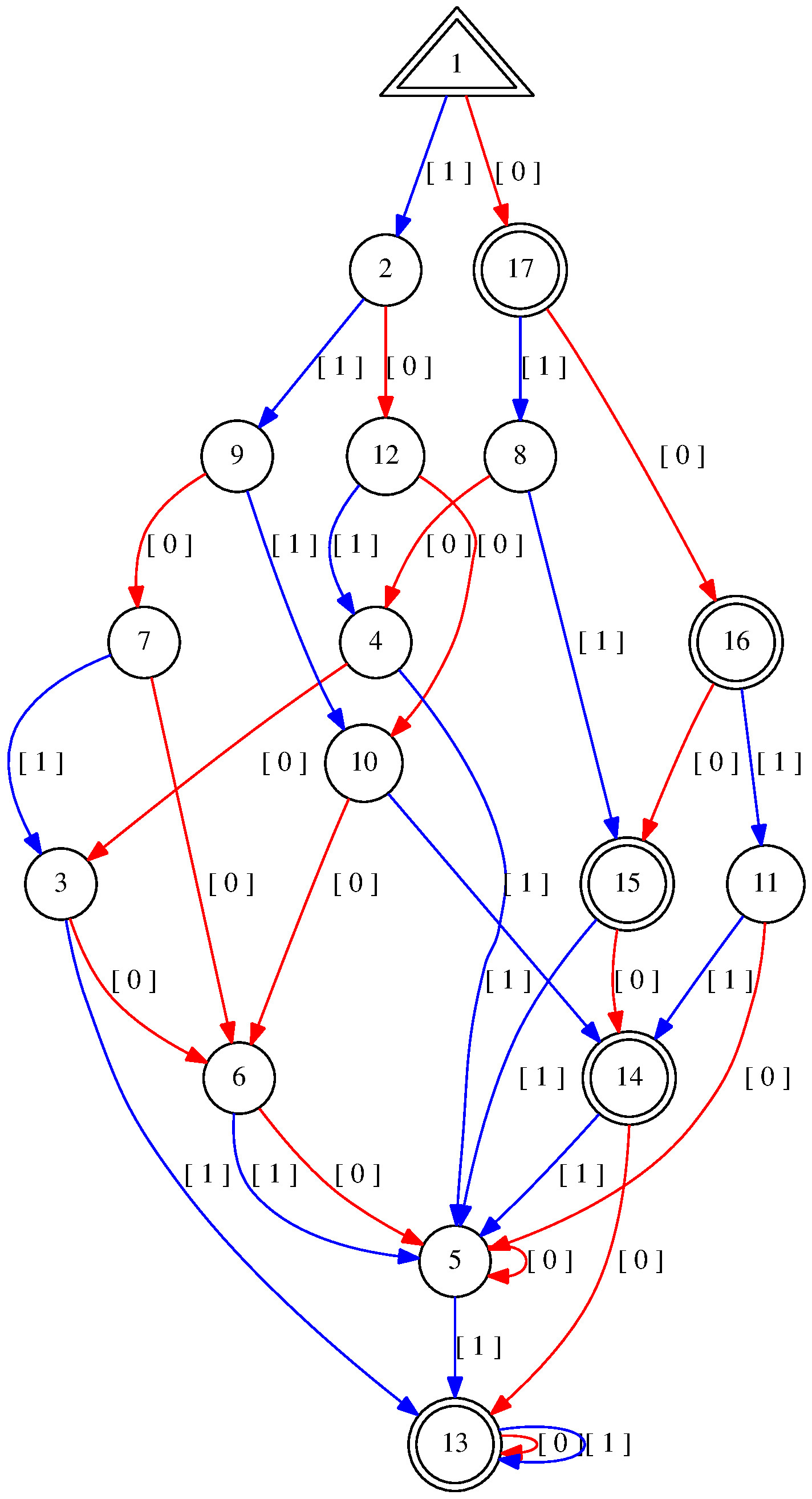
We recall the example from the section 1. There we wanted to get the Predicaton recognizing all natural numbers which can be purchased by 6, 9 and 20.
gap> # We create the Predicaton of the following formula gap> A:=Predicaton("(E x:(E y:(E z:6*x+9*y+20*z=n)))"); Predicaton: deterministic finite automaton on 2 letters with 17 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 --------------------------------------------------------------- [ 0 ] | 17 12 6 3 5 5 6 4 7 6 5 10 13 13 14 15 16 [ 1 ] | 2 9 13 5 13 5 3 15 10 14 14 4 13 5 5 11 8 Initial states: [ 1 ] Final states: [ 1, 13, 14, 15, 16, 17 ] The alphabet corresponds to the following variable list: [ "n" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 17 states and the variable position list [ 1 ]. > gap> Display(A); Predicaton: deterministic finite automaton on 2 letters with 17 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 --------------------------------------------------------------- [ 0 ] | 17 12 6 3 5 5 6 4 7 6 5 10 13 13 14 15 16 [ 1 ] | 2 9 13 5 13 5 3 15 10 14 14 4 13 5 5 11 8 Initial states: [ 1 ] Final states: [ 1, 13, 14, 15, 16, 17 ] The alphabet corresponds to the following variable list: [ "n" ]. gap> # We ask for the accepted natural numbers. gap> AcceptedByPredicaton(A, 20); [ [ 0 ], [ 6 ], [ 9 ], [ 12 ], [ 15 ], [ 18 ], [ 20 ] ] gap> DisplayAcceptedByPredicaton(A, 99, true); If the following words are accepted by the given automaton, then: Y, otherwise if not accepted: n. 0: Y 1: n 2: n 3: n 4: n 5: n 6: Y 7: n 8: n 9: Y 10: n 11: n 12: Y 13: n 14: n 15: Y 16: n 17: n 18: Y 19: n 20: Y 21: Y 22: n 23: n 24: Y 25: n 26: Y 27: Y 28: n 29: Y 30: Y 31: n 32: Y 33: Y 34: n 35: Y 36: Y 37: n 38: Y 39: Y 40: Y 41: Y 42: Y 43: n 44: Y 45: Y 46: Y 47: Y 48: Y 49: Y 50: Y 51: Y 52: Y 53: Y 54: Y 55: Y 56: Y 57: Y 58: Y 59: Y 60: Y 61: Y 62: Y 63: Y 64: Y 65: Y 66: Y 67: Y 68: Y 69: Y 70: Y 71: Y 72: Y 73: Y 74: Y 75: Y 76: Y 77: Y 78: Y 79: Y 80: Y 81: Y 82: Y 83: Y 84: Y 85: Y 86: Y 87: Y 88: Y 89: Y 90: Y 91: Y 92: Y 93: Y 94: Y 95: Y 96: Y 97: Y 98: Y 99: Y gap> # We create the Predicaton accepting the greatest non-accepted number. gap> # First we create a PredicatonRepresentation, containing a name, gap> # an arity and an automaton (the input may also be a Predicaton). gap> p:=PredicatonRepresentation("P", 1, A); < Predicaton represented with the name "P", the arity 1 and the deterministic automaton on 2 letters and 17 states. > gap> AddToPredicataList(p); gap> PredicataList; < PredicataRepresentation containing the following predicates: [ "P" ]. > gap> B:=Predicaton("(A m: m > n implies P[m]) and not P[n]"); Predicaton: deterministic finite automaton on 2 letters with 8 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 ------------------------------------ [ 0 ] | 2 2 2 3 2 5 2 8 [ 1 ] | 7 2 8 2 4 2 6 2 Initial states: [ 1 ] Final states: [ 8 ] The alphabet corresponds to the following variable list: [ "n" ]. Regular expression of the automaton: [ 1 ][ 1 ][ 0 ][ 1 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 8 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(B, 50); [ [ 43 ] ] gap> # We look at the regular expression and compute the natural number gap> PredicatonToRatExp(B); [ 1 ][ 1 ][ 0 ][ 1 ][ 0 ][ 1 ][ 0 ]* gap> BinToDec([ 1, 1, 0, 1, 0, 1 ]); 43 gap> # Alternatively, we can also use the inbuilt function: gap> C:=GreatestNonAcceptedNumber(A); Predicaton: deterministic finite automaton on 2 letters with 8 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 ------------------------------------ [ 0 ] | 2 2 2 3 2 5 2 8 [ 1 ] | 7 2 8 2 4 2 6 2 Initial states: [ 1 ] Final states: [ 8 ] The alphabet corresponds to the following variable list: [ "n" ]. Regular expression of the automaton: [ 1 ][ 1 ][ 0 ][ 1 ][ 0 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 8 states and the variable position list [ 1 ]. >
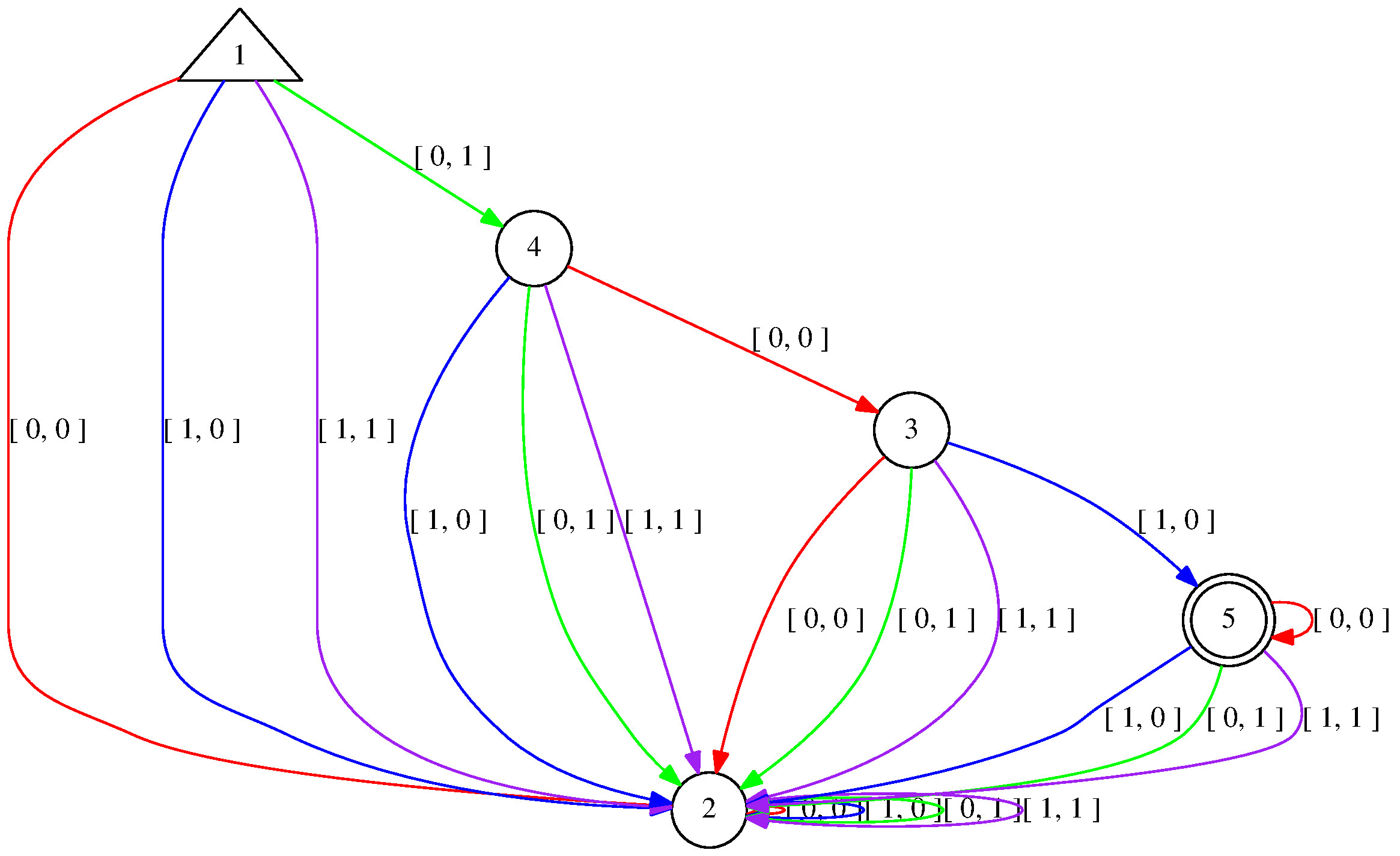
A. A very common example from an automata theory lecture is finding the natural numbers which are divisible by three. Sometimes this example is solve with clear rules, sometimes with a lot of handwaving.
However, the following way is a solid approach in the first-order language with \(+\) using the shortcut 3*x:=x+x+x.
Here, first the Predicaton for 3*y=x is created with the transition rule with the k-th state having carry (k-1): 3*a[1]=a[2]+(i-1)+2*((j-1)-(i-1)). For the existence quantifier we ignore the second component of each letter, which yields a nondeterministic finite automaton. We apply the leading zero completion (see NormalizedLeadingZeroPredicaton (2.3-12)), i.e. any leading zero may be cancelled or added to the accepted words. Then we apply the subset construction and return the minimal automaton.
gap> # We ask if there exists "y" s.t. 3*y=x. gap> A:=Predicaton("(E y: 3*y = x)"); Predicaton: deterministic finite automaton on 2 letters with 3 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 --------------------- [ 0 ] | 1 3 2 [ 1 ] | 2 1 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: ([ 1 ]([ 0 ][ 1 ]*[ 0 ])*[ 1 ]U[ 0 ])* Output: < Predicaton: deterministic finite automaton on 2 letters with 3 states and the variable position list [ 1 ]. > gap> # Compare with: gap> B:=Predicaton("3*y = x"); Predicaton: deterministic finite automaton on 4 letters with 4 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 --------------------------- [ 0, 0 ] | 1 2 2 3 [ 1, 0 ] | 2 2 1 2 [ 0, 1 ] | 2 2 4 2 [ 1, 1 ] | 3 2 2 4 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. Regular expression of the automaton: ([ 1, 1 ]([ 0, 1 ][ 1, 1 ]*[ 0, 0 ])*[ 1, 0 ]U[ 0, 0 ])* Output: < Predicaton: deterministic finite automaton on 4 letters with 4 states and the variable position list [ 1, 2 ]. > gap> Display(B); Predicaton: deterministic finite automaton on 4 letters with 4 states, the variable position list [ 1, 2 ] and the following transitions: | 1 2 3 4 --------------------------- [ 0, 0 ] | 1 2 2 3 [ 1, 0 ] | 2 2 1 2 [ 0, 1 ] | 2 2 4 2 [ 1, 1 ] | 3 2 2 4 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x", "y" ]. gap> C:=ExistsPredicaton(B, "y");; gap> Display(C); Predicaton: deterministic finite automaton on 2 letters with 3 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 --------------------- [ 0 ] | 1 3 2 [ 1 ] | 2 1 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x" ]. gap> DrawPredicaton(A);
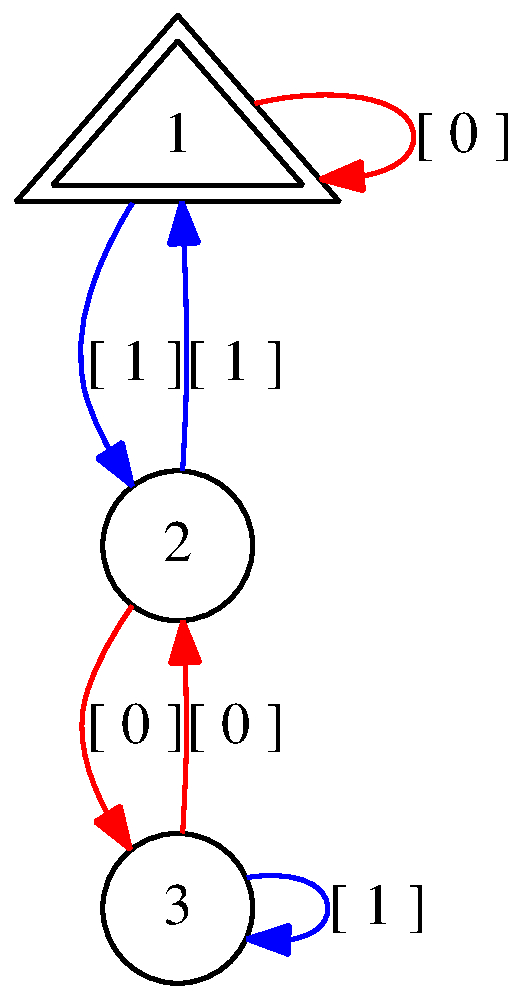
We can solve the linear congruences \(4\cdot x=7\) modulo 5 in the natural numbers.
gap> A:=Predicaton("(E y: 4*x = 7+5*y)"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 1 2 3 5 [ 1 ] | 2 5 1 4 3 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(A, 20); [ [ 3 ], [ 8 ], [ 13 ], [ 18 ] ] gap> # We asked for some accepted words and suggest as a solution x = 3+5*k. gap> B:=Predicaton("(E k: x = 3+5*k)"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 4 1 2 3 5 [ 1 ] | 2 5 1 4 3 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> # Indeed: gap> AreEquivalentPredicata(A, B); The Predicaton holds for all natural numbers and is interpreted as True. true gap> DrawPredicaton(A); gap> # Furthermore, we look at a system of linear congruences. gap> C:=Predicaton("(E y1: x = 1 + 2*y1) and (E y2: x = 2 + 3*y2)"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 2 2 4 3 5 [ 1 ] | 4 2 5 4 3 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 1 ][ 1 ]*[ 0 ]([ 1 ][ 0 ]*[ 1 ]U[ 0 ][ 1 ]*[ 0 ])*[ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(C, 20); [ [ 5 ], [ 11 ], [ 17 ] ] gap> # We suggest: gap> D:=Predicaton("(E k: x = 5 + 6 * k)"); Predicaton: deterministic finite automaton on 2 letters with 5 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 --------------------------- [ 0 ] | 2 2 4 3 5 [ 1 ] | 4 2 5 4 3 Initial states: [ 1 ] Final states: [ 5 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 1 ][ 1 ]*[ 0 ]([ 1 ][ 0 ]*[ 1 ]U[ 0 ][ 1 ]*[ 0 ])*[ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 5 states and the variable position list [ 1 ]. > gap> AreEquivalentPredicata(C, D); The Predicaton holds for all natural numbers and is interpreted as True. true
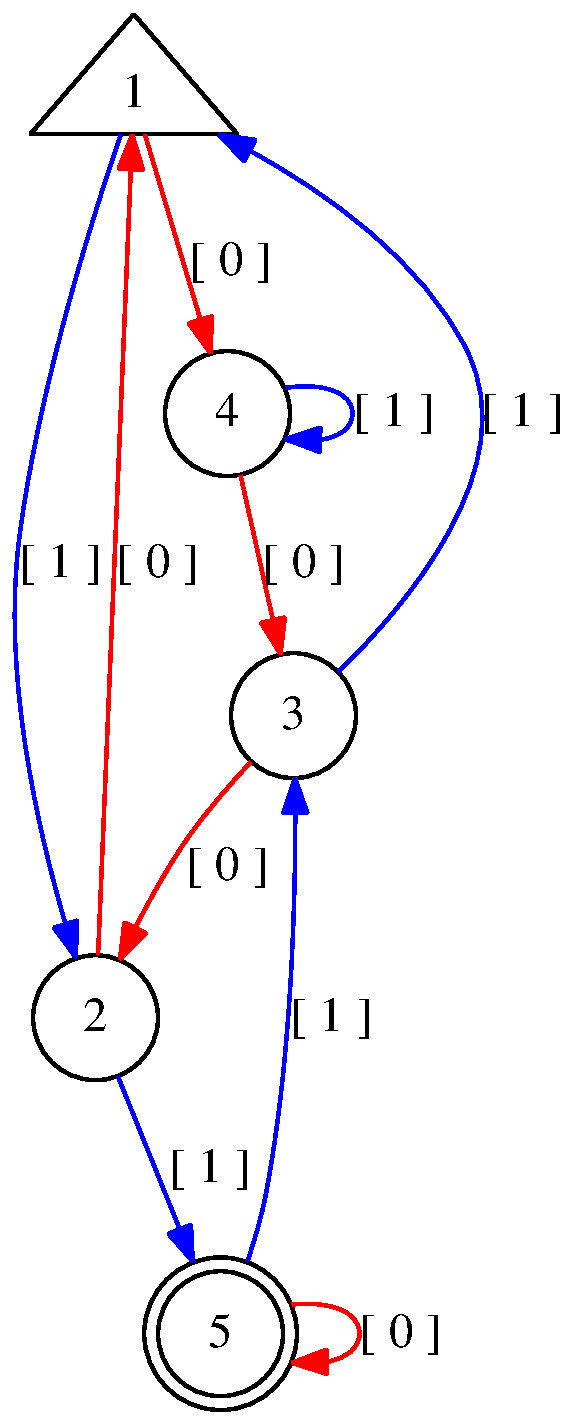
A. We can also compute the GCD and LCM of two natural numbers, however at the first sight it's not completely obvious how to obtain the GCD.
gap> # All multiples of the GCD of 6 and 15. If there exists z such that gap> # it is a multiple of the GCD(6, 15) after some number y, then also gap> # z+x is a multiple of the GCD. gap> A:=Predicaton("(E y: (A z: z>=y implies ((Ea : (Eb: z= 6*a+15*b))\ > implies (Ec: (Ed: z+x= 6*c+15*d)))))"); Predicaton: deterministic finite automaton on 2 letters with 3 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 --------------------- [ 0 ] | 1 3 2 [ 1 ] | 2 1 3 Initial states: [ 1 ] Final states: [ 1 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: ([ 1 ]([ 0 ][ 1 ]*[ 0 ])*[ 1 ]U[ 0 ])* Output: < Predicaton: deterministic finite automaton on 2 letters with 3 states and the variable position list [ 1 ]. > gap> # This Predicaton is already known from Example 2 and we test for the least gap> # accepted natural number greater 0 (>= 0 with optional parameter false): gap> B:=LeastAcceptedNumber(A); Predicaton: deterministic finite automaton on 2 letters with 4 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 ------------------------ [ 0 ] | 2 2 2 4 [ 1 ] | 3 2 4 2 Initial states: [ 1 ] Final states: [ 4 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 1 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 4 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(B); [ [ 3 ] ] gap> # We get the multiples of the LCM(6, 15) straightforwardly. gap> C:=Predicaton("(E a: 6*a = x) and (E b: 15*b = x)"); Predicaton: deterministic finite automaton on 2 letters with 17 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 --------------------------------------------------------------- [ 0 ] | 17 2 6 3 4 5 10 7 8 9 12 11 16 13 14 15 17 [ 1 ] | 2 2 17 6 7 13 5 3 11 16 10 4 12 8 15 9 14 Initial states: [ 1 ] Final states: [ 1, 17 ] The alphabet corresponds to the following variable list: [ "x" ]. Output: < Predicaton: deterministic finite automaton on 2 letters with 17 states and the variable position list [ 1 ]. > gap> D:=LeastAcceptedNumber(C); Predicaton: deterministic finite automaton on 2 letters with 7 states, the variable position list [ 1 ] and the following transitions: | 1 2 3 4 5 6 7 --------------------------------- [ 0 ] | 6 2 2 2 2 2 7 [ 1 ] | 2 2 7 3 4 5 2 Initial states: [ 1 ] Final states: [ 7 ] The alphabet corresponds to the following variable list: [ "x" ]. Regular expression of the automaton: [ 0 ][ 1 ][ 1 ][ 1 ][ 1 ][ 0 ]* Output: < Predicaton: deterministic finite automaton on 2 letters with 7 states and the variable position list [ 1 ]. > gap> AcceptedByPredicaton(D, 100); [ [ 30 ] ]
gap> # Which of the followings sentences are true? gap> A1:=Predicaton("(E x:(A y: x = y))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ ] Regular expression of the automaton: empty_set Due to the automaton the formula is false. false Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> A2:=Predicaton("(A x:(E y: x = y))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ] Regular expression of the automaton: [ ]* Due to the automaton the formula is true. true Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> A3:=Predicaton("(A x:(E y: x = y+1))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ ] Regular expression of the automaton: empty_set Due to the automaton the formula is false. false Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> A4:=Predicaton("(A x:(E y: x = 2*y) or (E y: x=2*y+1))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ] Regular expression of the automaton: [ ]* Due to the automaton the formula is true. true Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> A5:=Predicaton("(A n:(E n0: n > n0 implies (E x: (E y: 5*x+6*y=n))))"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ] Regular expression of the automaton: [ ]* Due to the automaton the formula is true. true Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. > gap> # Furthermore, we can use "true" and "false" as predicates; gap> A6:=Predicaton("true and (false implies true) implies true"); Predicaton: deterministic finite automaton on 1 letter with 1 state, the variable position list [ ] and the following transitions: | 1 ------------- [ ] | 1 Initial states: [ 1 ] Final states: [ 1 ] Regular expression of the automaton: [ ]* Due to the automaton the formula is true. true Output: < Predicaton: deterministic finite automaton on 1 letter with 1 state and the variable position list [ ]. >
generated by GAPDoc2HTML