A. Version 1.0
October 1, 2018
Fritz Kliemann
Email: fritz.kliemann@gmx.at
Address:
Linz, Austria
Status:
Not submitted
J. Shallit has successfully used automata theory to find properties of automatic sequences [Sha13]. In a summer school course at RISC, JKU Linz [AEC16], he explained also how to use finite automata to decide Presburger arithmetic [Pre29].
This package, written as a Master thesis, implements the decision procedure which goes back to J. R. Büchi [Büc60]. Furthermore, it allows to construct a deterministic finite automaton from any first-order formula with the addition as the only operation.
The package Automata [DLM11] is used for the data structure of finite automata.
© 2018 by Fritz Kliemann
This package may be redistribute and/or modify under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
WriteGapIniFile(); to get the right directory).LoadPackage("Predicata");I would like to thank my supervisor Erhard Aichinger for the opportunity to write this package and my parents for their support and patience.
The work was partially supported by the Austrian Science Fund (FWF), P29931.
The possibilities of the package Predicata, a combination of the words predicate and automata, can be best described with the following example.
For which natural numbers \(n\) does the formula, describing the McNuggets numbers,
\[\exists x: \exists y: \exists z: 6 \cdot x+9 \cdot y+20 \cdot z=n\]
hold? Furthermore, denoting the previous formula as \(P[n]\), for which natural number \(n\) does
\[(\forall m: m > n \Rightarrow P[m]) \wedge \neg P[n]\]
hold?
The idea is to create a deterministic finite automaton which corresponds to a first-order formula such that upon interpretation of every accepted word of the automaton the first-order formula is satisfied (Automata theory: [HMU01], [Pip97], [Koz97]).
The main object type Predicaton consists of an automaton and a list and represents first-order formulas containing the nullary operations \(0\) and \(1\) and the binary operation \(+\). A first-order formula with \(n\) different free variables, where each free variable is assigned to pairwise distinct natural numbers, is represented by an automaton over the alphabet \(\{0,1\}^n\). The variables are stored internally as a list of these \(n\) natural numbers, where the list coincides with the letters. The \(i\)-th position in a letter, i.e. in the \(n\)-tuple, corresponds to the variable at the \(i\)-th position in the list, i.e. to the variable which is assigned to the natural number at the \(i\)-th position. Leaving this technical details aside, the object type Predicaton (chapter 4) can also be called with a mathematically more intuitive first-order formula, which internally creates the deterministic finite automaton and takes care of the variables.
The special case are the first-order formulas with no free variable which can be seen as deterministic finite automaton with one state. This deterministic finite automatons can be either interpreted as True if the only state is a final state or as False otherwise. Thus this procedure, going back to J. R. Büchi ([Büc60]), decides the Presburger arithmetic (by Mojżesz Presburger, 1929, [Pre29]), the first-order theory of the natural numbers with the operation \(+\).
For first-time users it is recommended to start with Chapter 4, especially to start with the examples. The structure of the manual follows the structure of the package, thus the Chapter 2 and Chapter 3 gives insight on how in the background a first-order formula is transferred into deterministic finite automaton. However this is quite lengthy and definitely not recommended to begin with.
Hence it's more interesting to start with the example from above:
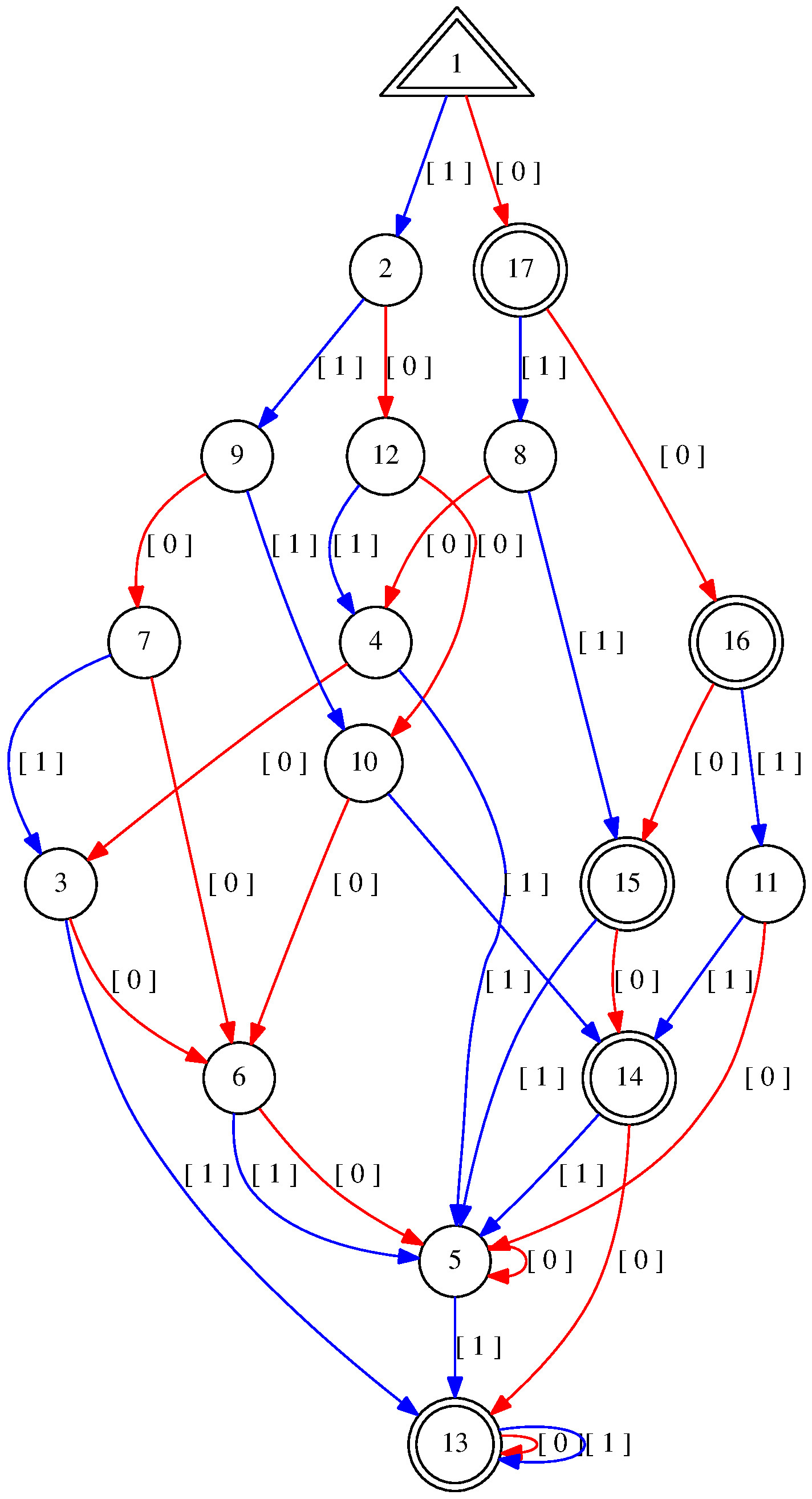
We start with A:=Predicaton("(E x:(E y:(E z:6*x+9*y+20*z=n)))");, consisting of a deterministic finite automaton with 17 states. The deterministic finite automaton displays the alphabet on the left, the states on the top, the transitions as entries in the table and the initial and final states at the bottom.
Furthermore we can also display the Predicaton anytime with: Display(A);. Additionally, we can draw it with DrawPredicaton(A);, using the external program graphviz (for requirements refer to the manual of the package Automata).
We can also test for accepted natural numbers with AcceptedByPredicaton(A, 20); where the optional second parameter gives an upper bound. DisplayAcceptedByPredicaton(A, 99); prints the accepted words converted into natural numbers in a nice format.
To conclude with the example, we ask for the greatest natural number which cannot be purchased with the function B:=GreatestNonAcceptedNumber(A); and test for AcceptedWordsByPredicaton(B, 50); or sum up the regular expression PredicatonToRatExp(B) (note: here the binary representation is read form behind.)

A. [AEC16] 3rd Algorithmic and Enumerative Combinatorics Summer School 2016 (2016) (Accessed: 2018-07-01), https://www.risc.jku.at/conferences/aec2016/.
[Büc60] Büchi, J. R., Weak Second-Order Arithmetic and Finite Automata, Zeitschrift für mathematische Logik und Grundlagen der Mathematik 6 (6) (1960), 66–92.
[DEG+02] Dobkin, D., Ellson, J., Gansner, E., Koutsofios, E., North, S. and Woodhull, G., Graphviz – Graph Drawing Programs, AT&T Research and Lucent Bell Labs (2002), https://www.graphviz.org/.
[DLM11] Delgado, M., Linton, S. and Morais, J., Automata, A package on automata, Version 1.13 (2011) (Refereed GAP package), http://www.fc.up.pt/cmup/mdelgado/automata/.
[HMU01] Hopcroft, J. E., Motwani, R. and Ullman, J. D., Introduction to Automata Theory, Languages, and Computation, Cengage Learning, 2nd edition, Boston, MA, USA (2001).
[Koz97] Kozen, D. C., Automata and Computability, Springer-Verlag, 1st edition, Berlin, Heidelberg (1997).
[Pip97] Pippenger, N., Theories of Computability, Cambridge University Press, 1st edition, New York, NY, USA (1997).
[Pre29] Presburger, M., Über die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen, in welchem die Addition als einzige Operation hervortritt, in Comptes Rendus du I congrès de Mathématiciens des Pays Slaves, , Warszawa (1929), 92–101.
[Sha13] Shallit, J. (Bulatov, A. A. and Shur, A. M., Eds.), Decidability and Enumeration for Automatic Sequences: A Survey, in Computer Science – Theory and Applications, Springer-Verlag, Berlin, Heidelberg (2013), 49–63.
[Sta84] Stansifer, R., Presburger's Article on Integer Airthmetic: Remarks and Translation, Cornell University, Computer Science Department (TR84-639) (1984) (Accessed: 2018-07-01), https://cs.fit.edu/~ryan/papers/presburger.pdf.