


Next: Functions on groups.
Up: Most important results.
Previous: Structure theory.
Contents
In [#!BM:DMFP!#], T. Boykett and P. Mayr established a link from the various
sporadic classes of designs built from planar near-rings to the classical
theory of designs from difference families. They show that certain sets of
fixed-point-free automorphism groups on finite groups form so-called
short difference families. Thus they give a general framework to explain
the classical designs from near-rings as described by J. Clay and the segments
by Sun. Also a new class of BIB-designs with parameters
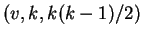 is obtained.
is obtained.
In [#!BM:FAGF!#], T. Boykett and P. Mayr showed that a large class of
planar near-rings (Ferrero pairs) is ring-generated. This means that the
additive group of the near-ring 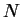 is that of a ring
is that of a ring 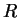 and that the
multiplication of
and that the
multiplication of 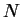 can be obtained by the multiplicative group of
can be obtained by the multiplicative group of 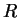 .
In this situation planar near-rings and hence designs can be easily obtained
from rings.
.
In this situation planar near-rings and hence designs can be easily obtained
from rings.
Peter Mayr
2005-11-25
![]() is that of a ring
is that of a ring ![]() and that the
multiplication of
and that the
multiplication of ![]() can be obtained by the multiplicative group of
can be obtained by the multiplicative group of ![]() .
In this situation planar near-rings and hence designs can be easily obtained
from rings.
.
In this situation planar near-rings and hence designs can be easily obtained
from rings.