


Next: Designs.
Up: Most important results.
Previous: Most important results.
Contents
G. Wendt showed that every finite planar near-ring occurs, up to isomorphism,
as a subnear-ring of a centralizer near-ring [#!We:CRFP!#].
Conversely, minimal left ideals of 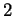 -primitive near-rings are planar
near-rings.
More generally, any near-ring with a multiplicative right identity can be
described as centralizer near-ring in which the multiplication is not
composition of functions but a so-called sandwich
multiplication [#!We:PNSN!#]. This description is one of the most
interesting structural results obtained since it provides a new method to
study near-rings with right identity more closely (for example: primitive
near-rings, planar near-rings).
The question whether a near-ring has a multiplicative right identity or not
was the motivation to investigate near-rings with the focus on their
multiplicative semigroups
in [#!We:OTMS!#].
In this area, G. Wendt also obtained general results on zero divisors in
near-rings [#!We:OTNO!#], on the multiplicative behaviour of near-rings
in general, and on the multiplicative semigroup of subnear-rings of
1-primitive near-rings [#!We:LII1!#].
-primitive near-rings are planar
near-rings.
More generally, any near-ring with a multiplicative right identity can be
described as centralizer near-ring in which the multiplication is not
composition of functions but a so-called sandwich
multiplication [#!We:PNSN!#]. This description is one of the most
interesting structural results obtained since it provides a new method to
study near-rings with right identity more closely (for example: primitive
near-rings, planar near-rings).
The question whether a near-ring has a multiplicative right identity or not
was the motivation to investigate near-rings with the focus on their
multiplicative semigroups
in [#!We:OTMS!#].
In this area, G. Wendt also obtained general results on zero divisors in
near-rings [#!We:OTNO!#], on the multiplicative behaviour of near-rings
in general, and on the multiplicative semigroup of subnear-rings of
1-primitive near-rings [#!We:LII1!#].
A different approach yielded a description of the maximal near-rings of
functions on finite groups. For a given finite group 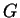 , it is now possible
to determine whether a given set of functions
, it is now possible
to determine whether a given set of functions 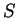 on
on 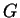 generates the
near-ring
generates the
near-ring 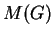 of all functions on
of all functions on 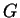 by checking whether
by checking whether 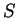 is contained
in any of the maximal subnear-rings of
is contained
in any of the maximal subnear-rings of 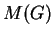 . This result was obtained
by E. Aichinger et al. using a combination of near-ring theory, clone theory,
and group theory [#!AM:CFCN!#]. As a consequence, they give a bound for the
probability
. This result was obtained
by E. Aichinger et al. using a combination of near-ring theory, clone theory,
and group theory [#!AM:CFCN!#]. As a consequence, they give a bound for the
probability 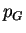 that a randomly chosen bijection on
that a randomly chosen bijection on 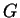 generates all of
generates all of
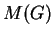 for
for 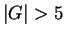 :
:
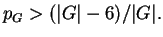
For
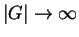 ,
, 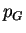 tends to
tends to 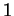 ;
in particular, this shows that on groups with at least
;
in particular, this shows that on groups with at least 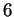 elements there
always exists a single bijection that generates all of
elements there
always exists a single bijection that generates all of 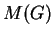 .
Depending on I. Rosenbergs famous characterization of maximal clones,
this result is in line with a growing number of recent results on the
probability that a randomly chosen element generates a given algebra
(group,...).
In his diploma thesis, C. Neumaier independently characterized the maximal
subnear-rings of the zero-symmetric functions
.
Depending on I. Rosenbergs famous characterization of maximal clones,
this result is in line with a growing number of recent results on the
probability that a randomly chosen element generates a given algebra
(group,...).
In his diploma thesis, C. Neumaier independently characterized the maximal
subnear-rings of the zero-symmetric functions 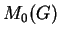 . By a careful analysis
of the involutions in
. By a careful analysis
of the involutions in 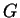 , he obtained generating probabilities in this case
[#!Ne:TMSO!#,#!Ne:TFOT!#].
, he obtained generating probabilities in this case
[#!Ne:TMSO!#,#!Ne:TFOT!#].
A third line of research on the structure of planar near-rings was positioned
around a question that was dubbed
``one of the most long-standing and probably most difficult in the vicinity of
near-ring theory'' by H. Kiechle in one of the main talks at the international
conference Near-rings and Near-fields 2005: Is every near-domain a near-field?
Equivalently, does every sharply 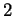 -transitive permutation group have a
regular normal subgroup?
Certain finiteness conditions are known to guarantee the existence of a
regular normal subgroup. P. Mayr proved that sharply
-transitive permutation group have a
regular normal subgroup?
Certain finiteness conditions are known to guarantee the existence of a
regular normal subgroup. P. Mayr proved that sharply 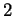 -transitive
permutation groups whose point stabilizer has exponent
-transitive
permutation groups whose point stabilizer has exponent 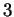 or
or 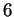 have such
a regular normal subgroup [#!Ma:S2TG!#].
Apart from near-ring theory, this result is of interest for classical group
theory.
As consequences, certain near-domains are in fact finite planar near-fields,
the varieties of zero-symmetric right near-rings with left identities
satisfying
have such
a regular normal subgroup [#!Ma:S2TG!#].
Apart from near-ring theory, this result is of interest for classical group
theory.
As consequences, certain near-domains are in fact finite planar near-fields,
the varieties of zero-symmetric right near-rings with left identities
satisfying 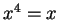 or
or 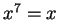 are varieties of commutative rings.
are varieties of commutative rings.



Next: Designs.
Up: Most important results.
Previous: Most important results.
Contents
Peter Mayr
2005-11-25
![]() , it is now possible
to determine whether a given set of functions
, it is now possible
to determine whether a given set of functions ![]() on
on ![]() generates the
near-ring
generates the
near-ring ![]() of all functions on
of all functions on ![]() by checking whether
by checking whether ![]() is contained
in any of the maximal subnear-rings of
is contained
in any of the maximal subnear-rings of ![]() . This result was obtained
by E. Aichinger et al. using a combination of near-ring theory, clone theory,
and group theory [#!AM:CFCN!#]. As a consequence, they give a bound for the
probability
. This result was obtained
by E. Aichinger et al. using a combination of near-ring theory, clone theory,
and group theory [#!AM:CFCN!#]. As a consequence, they give a bound for the
probability ![]() that a randomly chosen bijection on
that a randomly chosen bijection on ![]() generates all of
generates all of
![]() for
for ![]() :
:
![]() -transitive permutation group have a
regular normal subgroup?
Certain finiteness conditions are known to guarantee the existence of a
regular normal subgroup. P. Mayr proved that sharply
-transitive permutation group have a
regular normal subgroup?
Certain finiteness conditions are known to guarantee the existence of a
regular normal subgroup. P. Mayr proved that sharply ![]() -transitive
permutation groups whose point stabilizer has exponent
-transitive
permutation groups whose point stabilizer has exponent ![]() or
or ![]() have such
a regular normal subgroup [#!Ma:S2TG!#].
Apart from near-ring theory, this result is of interest for classical group
theory.
As consequences, certain near-domains are in fact finite planar near-fields,
the varieties of zero-symmetric right near-rings with left identities
satisfying
have such
a regular normal subgroup [#!Ma:S2TG!#].
Apart from near-ring theory, this result is of interest for classical group
theory.
As consequences, certain near-domains are in fact finite planar near-fields,
the varieties of zero-symmetric right near-rings with left identities
satisfying ![]() or
or ![]() are varieties of commutative rings.
are varieties of commutative rings.