What we intend to do

We intend to produce a library of functions for working with near-rings. This library shall be built upon the group-theory system GAP (cf. [S 94]). For this purpose, algorithms for computing with near-rings have to be developed further. The resulting package will then be used for treating some questions in the theory of function near-rings, such as the description of affine complete groups (at least for some classes of groups) or of those near-rings that have a distributive lattice of left ideals. Since complete solutions to these problems still seem very far, also examples and partial solutions would be interesting.

Prototypes for this GAP-library do already exist and the first results which we have presented at the international conference on near-rings and near-fields at Hamburg this summer have raised great interest of the researchers in near-ring theory. With our approach we have already significantly pushed ahead the the size of the near-rings we are able to investigate. At this point we only want to state two examples:

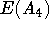• Using our methods, it took us 3 seconds to compute the size of the endomorphism near-ring . This near-ring has 196608 elements (cf. [FK95]). It takes us 15 s to compute the size of the near-ring 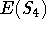(which is 927712935936).
• A group is called affine complete if any congruence-preserving function is a polynomial function. Quite a number of groups are known to be affine complete (cf. [Kaa78], [Kaa82]). Using our programs, we have been able to find all non-abelian affine complete groups of order less than 31: the groups 16/6, 16/7 and 18/5 (the names of the groups are chosen according to [TW80]). Only for the group 16/7 there exists a (previously published) proof for the affine completeness.

The crucial points of this project are therefore the following steps:

1. Development of good data-structures for representing near-rings and of efficient algorithms for computing with these representations.
2. Implementation of these algorithms on top of GAP. The near-rings package that we will write shall meet the (high) standards of the GAP-people as to:
   1. Formal quality of the source code (documentation, readability, ...).
   2. User-friendliness of the resulting functions.
3. Investigation of some problems related to function near-rings, especially of those problems related to interpolation theory.

Using our package, the user will be able to compute the following near-rings:

1. polynomial functions (P(G))
2. endomorphism near-rings (I(G), A(G), E(G))
3. centralizer near-rings ( )

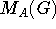Once these near-rings are constructed, the user can e.g. compute the following structures:

1. Ideals (left, right)
2. Noetherian Quotients

On top of this package, we plan to implement some of the more applied features of near-ring theory, such as the constructions of BIB-designs and codes (cf. [Cla92]).