Preparatory work for the programming part

1. Christof Nöbauer has implemented Yearby's algorithm ([Yea73]) for providing a GAP-library of all near-rings of order less than 16. Together with this library he wrote a lot of functions for investigating small near-rings and searching through the library. This work can be found in his diploma thesis [Nöb95].
2. Jürgen Ecker is currently working on his diploma thesis, trying to find methods for factoring rings into subdirectly irreducble components and to provide a set of basic functions for computing with rings. He is implementing his methods in GAP. The following shall give some insight into his work:

   We start with the group G8/2 (classification according to [TW80]), which is and construct, as a very easy example, the zero-ring on this group.

   gap> ZR8_2 := AsRing(G8_2,zero);
   RingfromGroup(G8/2 , function ( x, y )
       return ();
   end
   gap> ZR8_2.name := "ZR8/2";
   "ZR8/2"

   We can easily analyze the ideal structure of this ring.

   gap> I := Ideals(ZR8_2);
   [ Ideal ( ZR8/2 , [] ), Ideal ( ZR8/2 , (5,6) ), 
     Ideal ( ZR8/2 , (1,2,3,4) , (5,6) ), Ideal ( ZR8/2 , (5,6) , (1,3)(2,4) ), 
     Ideal ( ZR8/2 , (1,3)(2,4) , (1,2,3,4) ), 
     Ideal ( ZR8/2 , (1,3)(2,4) , (1,2,3,4)(5,6) ), Ideal ( ZR8/2 , (1,3)(2,4) ),
     Ideal ( ZR8/2 , (1,3)(2,4)(5,6) ) ]

   From a ring and an ideal we construct the factor-ring.

   gap> F := ZR8_2 / I[2];
   FactorRing ( ZR8/2 , Ideal ( ZR8/2 , (5,6) ) )
   gap> Elements(F);
   [ FactorRingElement ( () + Ideal ( ZR8/2 , (5,6) ) ), 
     FactorRingElement ( (1,2,3,4) + Ideal ( ZR8/2 , (5,6) ) ), 
     FactorRingElement ( (1,3)(2,4) + Ideal ( ZR8/2 , (5,6) ) ), 
     FactorRingElement ( (1,4,3,2) + Ideal ( ZR8/2 , (5,6) ) ) ]

   The result is again a ring. We continue investigating this factor-ring:

   gap> IsSimple(F);
   false

3. Erhard Aichinger: I have written a small prototype for the system to be realized in this project. These functions were initially only meant to test some of my conjectures. They have then become so interesting to me and to other researchers in near-ring theory to whom I showed them that I finally realized that ``computational near-ring theory'' is worth being developed further and that the outcome should be a system for working with near-rings on a computer. Based also on [Nöb95], I have already computed a list of the cardinalities of the endomorphism near-rings on small groups ([]). Furthermore, I want to show here some functions of the existing prototype:
   
   • Polynomial functions
     PG( G )
     The function PG computes the nearring of polynomial functions on the group G.
     The group G24/12 is the group 24/12 in the classification of [TW80], namely the symmetric group on 4 letters.

     gap> P := PG (G24_12);
     P(G24/12)
     gap> Size (P);
     22265110462464

   • Endomorphism nearrings
     EG( G )
     The function EG computes the nearring additively generated by the endomorphisms on the group G, usually denoted by E(G).

     gap> E := EG (G24_12);
     E(G24/12)
     gap> Size (E);
     927712935936

   • Centralizer nearrings
     MsG( MG(G), S )
     The function MsG computes the centralizer nearring .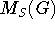

     gap> endo := Endomorphisms (G6_2);
     [ [ 1, 1, 1, 1, 1, 1 ] , [ 1, 2, 2, 1, 1, 2 ] , [ 1, 2, 6, 5, 4, 3 ] , 
       [ 1, 3, 2, 5, 4, 6 ] , [ 1, 3, 3, 1, 1, 3 ] , [ 1, 3, 6, 4, 5, 2 ] , 
       [ 1, 6, 2, 4, 5, 3 ] , [ 1, 6, 3, 5, 4, 2 ] , [ 1, 6, 6, 1, 1, 6 ] , 
       [ 1, 2, 3, 4, 5, 6 ]  ]
     gap> Mend := MsG ( MG (G6_2), endo );;
     gap> PrintNr (Mend);
     
     F : Subgroup( Group( (1,2), (1,2,3), (4,5), (4,5,6), (7,8), (7,8,9), (10,11), 
     (10,11,12), (13,14), (13,14,15), (16,17), (16,17,18) ), 
     [ (10,11,12)(13,15,14), ( 5, 6)( 7, 8)(16,18) ] )
      Size : 6
     
     G : 6/2
      Size : 6
     
     -------------------------------
     Elements of G
      [ (), (2,3), (1,2), (1,2,3), (1,3,2), (1,3) ]
     -----------------------------------------
     The additive group of F is generated by
     -----------------------------------------
     
      f: [ (), (), (), ( 1, 2, 3), ( 1, 3, 2), () ]
     
      f: [ (), (2,3), (1,2), (), (), ( 1, 3) ]
     -----------------------------------------
     
     gap> Size (Mend);
     6

   • Compatible functions
     A function on a group G is compatible iff it can be interpolated by a polynomial function at each subset of G with at most two elements. Following this, we compute the compatible functions on the cyclic group with 11 elements. The function LocalNr ( nr, t ) computes the near-ring of all functions that can be interpolated by a function in the nearring nr at each subset of at most t elements.

     gap> P := PG (G11_1);
     P(11/1)
     gap> Size (P);
     121
     gap> C := LocalNr (P, 2);
     L_2 P(11/1)
     gap> Size (C);
     285311670611

   • Ideals
     LeftIdeals( nr )
     The function LeftIdeals computes the lattice of left ideals of the nearring nr.

     gap> P := PG (G6_2);
     P(6/2)
     gap> L := LeftIdeals (P);
     [ Subgroup( Group( (1,2), (1,2,3), (4,5), (4,5,6), (7,8), (7,8,9), (10,11), 
         (10,11,12), (13,14), (13,14,15), (16,17), (16,17,18) ), [  ] ), 
       Subgroup( Group( (1,2), (1,2,3), (4,5), (4,5,6), (7,8), (7,8,9), (10,11), 
         (10,11,12), (13,14), (13,14,15), (16,17), (16,17,18) ), 
         [ (10,11,12)(13,15,14) ] ), Subgroup( Group( (1,2), (1,2,3), (4,5), 
         (4,5,6), (7,8), (7,8,9), (10,11), (10,11,12), (13,14), (13,14,15), 
         (16,17), (16,17,18) ), [ ( 7, 8, 9)(16,18,17) ] ), .....

     This is the internal representation of left ideals. Now we look how many left ideals there are.

       
     gap> Length (L);
     50

     Is the lattice of left ideals distributive ?

     gap> IsDistributive (L);
     false

   • Noetherian Quotients
     NoetherianQuotient ( nr, , )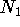
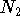     If nr is a nearring of functions on the group G,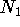 is a subgroup of G and 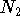is a subset of G, then this function returns the set of all functions in nr that map 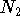into .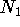

     gap> P := PG (G24_12);
     P(G24/12)
     gap> N := NoetherianQuotient (P, A4, G);;
     gap> Size (N);
     5566277615616
     gap> N2 := NoetherianQuotient (P, TrivialSubgroup (G24_12), A4);;
     gap> Size (N2);
     4718592
     gap> N2 := NoetherianQuotient (P, TrivialSubgroup (G24_12), G);;
     gap> Size (N2);
     1

The resulting system will therefore at least contain the functions described in the last two sections.