

Nächste Seite: Literatur
Aufwärts: Themen für Seminar-, Magister-
Vorherige Seite: Kontaktpersonen
Unterabschnitte
Für eine endliche Gruppe
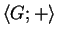 ist
ist
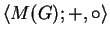 der Fastring aller Funktionen auf
der Fastring aller Funktionen auf 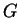 .
In dieser Arbeit sollen Methoden untersucht werden,
die Größe des von einigen Funktionen
.
In dieser Arbeit sollen Methoden untersucht werden,
die Größe des von einigen Funktionen
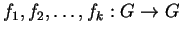 erzeugten Unterfastrings von
erzeugten Unterfastrings von 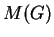 algorithmisch
zu bestimmen.
Dabei sollen Algorithmen gefunden werden, die
für kleine Gruppen (weniger als 100 Elemente) und
wenige erzeugende Funktionen schnell laufen.
Man weiß zum Beispiel, dass eine zufällig ausgewählte
Funktion von
algorithmisch
zu bestimmen.
Dabei sollen Algorithmen gefunden werden, die
für kleine Gruppen (weniger als 100 Elemente) und
wenige erzeugende Funktionen schnell laufen.
Man weiß zum Beispiel, dass eine zufällig ausgewählte
Funktion von 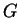 nach
nach 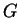 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit
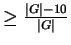 den gesamten Fastring
den gesamten Fastring
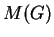 erzeugt [AMPW02].
erzeugt [AMPW02].
Eine Einführung bieten die Arbeiten
[AEN01,BAE$^+$00,BM01].
Zur Lösung des Problems gibt es bisher zwei Ansätze:
- eine probabilistische Methode [AEN01]:
Anstatt zu testen, ob eine erzeugte Menge von
Funktionen ageschlossen bezüglich
Hintereinanderausführung ist, testet diese
Methode nur die Hintereinanderausführung
einiger weniger Paare von Funktionen.
Es geht jetzt darum, untere Schranken für
die Wahrscheinlichkeit zu finden, dass man
mit dieser Methode gegebenfalls tatsächlich einen
Zeugen für die Nichtabgeschlossenheit
bezüglich der Hintereinanderausführung findet.
- Da es einfach ist, den additiven Abschluss
von Funktionen zu berechnen (die algorithmische
Gruppentheorie [GAP99] kann das), wäre
es günstig, additive Generatoren des Fastringes
zu finden (cf. [AEN01]). Das ist für
distributiv erzeugte Fastringe einfach.
Nach einer Idee von F. Binder ist eine
Verallgemeinerung vielleicht mithilfe
des Differenzenoperators [BM01] für
``fast distributiv'' erzeugte Fastringe möglich.
Die entworfenen Lösungsstrategien sollen in SONATA [ABE$^+$99]
implementiert und verglichen werden.
In [AI01] wurden alle endlichen 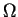 -Gruppen
bestimmt, für die jede unäre (nicht notwendigerweise überall
definierte) kongruenzerhaltende Funktion eine Polynomfunktion
ist; solche
-Gruppen
bestimmt, für die jede unäre (nicht notwendigerweise überall
definierte) kongruenzerhaltende Funktion eine Polynomfunktion
ist; solche 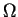 -Gruppen heißen
strikt lokal
-Gruppen heißen
strikt lokal 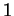 -affin vollständig.
Dabei wurden, als Nebenprodukt, alle
-affin vollständig.
Dabei wurden, als Nebenprodukt, alle 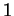 -affin vollständigen
-affin vollständigen
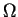 -Gruppen bestimmt, die eine bestimmte Bedingung
an den Idealverband erfüllen.
Die Beweismethoden erlauben vermutlich auch, zu zeigen,
dass jede
-Gruppen bestimmt, die eine bestimmte Bedingung
an den Idealverband erfüllen.
Die Beweismethoden erlauben vermutlich auch, zu zeigen,
dass jede 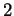 -affin vollständige
-affin vollständige 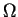 -Gruppe, die
diese Bedingung erfüllt, affin vollständig ist.
Das ist auszuführen.
-Gruppe, die
diese Bedingung erfüllt, affin vollständig ist.
Das ist auszuführen.
Literatur: [Aic02,AI01,KP01]
Der Polynomfastring
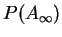 auf der Gruppe
auf der Gruppe
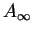 , der
unendlichen alternierenden Gruppe, hat eine
Menge interessanter Eigenschaften.
So ist
, der
unendlichen alternierenden Gruppe, hat eine
Menge interessanter Eigenschaften.
So ist
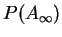 dicht in
dicht in
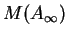 ,
sein nullsymmetrischer Teil
,
sein nullsymmetrischer Teil
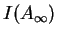 hat
unendlich viele maximale Ideale, ....
hat
unendlich viele maximale Ideale, ....
Die Funktionen, die in diesem Fastring liegen, lassen
sich vermutlich konkret beschreiben. Das ist auszuführen.
Daneben kann man vielleicht große Teile des
Idealverbands dieses Fastringes direkt bestimmen.
Literatur: [Sco69,Pil83].
Hanna Neumann [Neu56] hat 1956 eine Möglichkeit
angegeben, Endomorphismen auf bestimmten nichtabelschen
Gruppen so zu addieren, dass wieder ein Endomorphismus
herauskommt.
Diese Konstruktion ist für kleine Gruppen in SONATA
zu implementieren.
Das erfordert zunächst die Erzeugung der
freien Gruppe in der von einer gegeben Gruppe
erzeugten Varietät, also die Erzeugung
der Termfunktionen einer gegebenen Gruppe.
Dieser Teil bietet keine besonderen theoretischen
Schwierigkeiten.
Die erzeugten Fastringe sollen dann mithilfe von
SONATA untersucht werden.
Literatur:[Neu56], [Cla92, p.5].
Für einige Klassen von Codes (BCH-Codes, Reed-Muller-Codes)
sind die bekannten Decodieralgorithmen
darzustellen und der Aufwand beim Decodieren
zu ermitteln.
Diese Ergebnisse für diese Codes sind
mit den aus Fastringen erzeugten
Codes [FHP90] zu vergleichen.
Literatur: [Wil99,FHP90].
Kompositionsringe [Adl62] sind die
algebraischen Strukturen, die man beim
Studium von Funktionen auf Ringen erhält.
Kurioserweise kann ein Kompositionsring
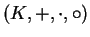 mit
mit
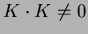 auch eine kommutative Multiplikation
auch eine kommutative Multiplikation
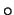 besitzen.
In [Aic97] wurden alle endlichen einfachen
Kompositionsringe bestimmt.
Es sollen nun (alle) Kompositionsringe
mit kommutativer Multiplikation
bestimmt werden.
besitzen.
In [Aic97] wurden alle endlichen einfachen
Kompositionsringe bestimmt.
Es sollen nun (alle) Kompositionsringe
mit kommutativer Multiplikation
bestimmt werden.
Literatur: [Adl62,Aic97,Pil83]


Nächste Seite: Literatur
Aufwärts: Themen für Seminar-, Magister-
Vorherige Seite: Kontaktpersonen
Erhard Aichinger
2003-05-06